Fizikai Szemle 2000/6. 181.o.

HOLOGRÁFIA, 1948-1971

A Nobel-díj átadásakor, 1971. december 11-én tartott előadás

Gábor Dénes
Imperial Collegium, London

Elődeimhez képest az az előnyöm előadásomban, hogy egyetlen egyenletet sem kell leírnom, egyetlen absztrakt ábrát sem kell bemutatnom. Természetesen szinte tetszőleges mennyiségű matematikát vezethetünk be a holográfiába, de a lényeg fizikai érvekkel megmagyarázható és megérthető.

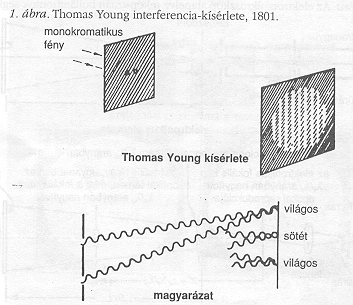
A holográfia a fény hullámtermészetén alapul, amit először Thomas Young demonstrált meggyőzően 1801-ben, egy csodálatosan egyszerű kísérlettel (1. ábra). Napsugarat bocsátott egy sötét szobába, útjába egy sötét ernyőt helyezett, rajta két tűszúrásnyi lyukkal, és ettől bizonyos távolságban egy fehér ernyőt. Két sötét vonalat látott egy fényes vonal két oldalán, ami annyira felbátorította, hogy megismételte a kísérletet. Fényforrásként ezúttal alkohollángot használt, benne egy kis sóval, hogy nátrium fényt tudjon előállítani. Most számos, szabályosan elhelyezkedő sötét vonalat látott. Ez volt az első világos bizonyíték arra, hogy ha fényhez fényt adunk, sötétséget kaphatunk. A jelenség neve interferencia. Thomas Young számított erre, mert hitt a fény hullámelméletében. Christian Huygens eredeti ötletéhez az volt a fő hozzájárulása, hogy a monokromatikus fény szabályos szinuszos rezgést jelent egy közegben, amelyet azidőtájt éternek hívtak. Ha ez így van, akkor lehetséges, hogy több fényt kapunk, ha hullámhegyhez hullámhegyet; és sötétséget, ha hullámhegyhez hullámvölgyet adunk.

Az interferenciára képes fényt “koherensnek" nevezzük. Nyilvánvaló, hogy sok interferenciavonal megjelenéséhez a fénynek nagyon monokromatikusnak kell lennie. A koherenciát szokás szerint az egyazon forrásból származó két sugár azon útkülönbségével mérjük, amiben különbözhetnek egymástól, hogy még megfigyelhető interferenciakontrasztot adjanak. Ez a koherenciahossz a holográfia elméletében és gyakorlatában egyaránt fontos mennyiség. Lord Rayleigh és Albert Michelson elsőként jöttek rá, hogy ez nem más, mint a spektroszkópiai vonalszélesség reciprok mértéke. Michelson a spektrálanalízis zseniális módszereiben és a csillagátmérők mérésében használta.

Ugorjunk most. másfél évszázadot, 1947-be. Ebben az időben nagyon érdekelt az elektronmikroszkópia. E nagyszerű készülék abban az időben a legjobb fénymikroszkópénál százszor jobb felbontást adott, ami mégis kiábrándító volt, mert megállt kevéssel az atomrácsok felbontása előtt. A gyors elektronok de Broglie-hullámhossza, körülbelül 0,005 nm, ami ugyan elég rövid, de az optika tökéletlen volt. Az elkészíthető legjobb elektronobjektív optikai tökéletessége inkább egy esőcseppéhez volt hasonlítható, mint egy mikroszkóp objektívéhez. O. Scherzer elméleti munkájából tudtu k, hogy ez nem is fokozható. Az elméleti határt akkoriban 0,4 nm-re becsülték, nagyjából kétszer akkorára, mint ami az atomrácsok felbontásához szükséges, a gyakorlati megvalósítás határa pedig körülbelül 1,2 nm-nél tartott. E határok abból adódtak, hogy az elektronlencsék aperturáját körülbelül 5/1000 radiánra kellett korlátoznunk. Ekkora szögnél a szférikus aberráció hibája nagyjából megegyezik a diffrakciós hibával. Ha megkétszerezzük ezt az aperturát, hogy a diffrakciós hiba feleződjék, a szférikus aberráció nyolcszorosra növekszik és a kép reménytelenül elmosódik.

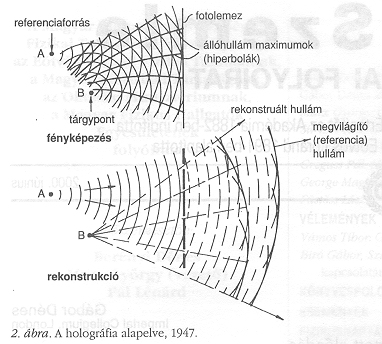A problémán való hosszas tűnődés után 1947-ben egy szép húsvéti napon hirtelen rájöttem egy megoldásra, ami a 2. ábrán látható. Miért nem készítünk rossz elektronképet, ami viszont tartalmazza a teljes információt, és amit aztán optikai eszközökkel korrigálunk? Világos volt számomra, hogy ha egyáltalán lehetséges, akkor csak koherens elektronnyalábokkal valósítható meg, olyan elektronhullámokkal, amelyek határozott fázissal rendelkeznek. A közönséges fénykép teljesen elveszíti a fázist, csak az intenzitásokat rögzíti. De ne csodálkozzunk azon, hogy elveszítjük a fázist, ha nincs mihez hasonlítanunk! Lássuk, mi történik, ha egy etalont, vagyis egy “koherens hátteret" adunk hozzá! Elgondolásomat a 2. ábra mutatja arra az egyszerű esetre, amikor csak egy tárgypont van. A tárgyhullám és a koherens háttér, vagy “referenciahullám" ekkor interferenciacsíkokat hoz létre. Maximumok jelentkeznek mindenhol, ahol a két hullám fázisa megegyezik. Készítsünk egy éles pozitív képet, amelyik csak a maximumoknál ereszt át, és világítsuk meg a referenciaforrással. A fázisok az A forrásra nézve természetesen helyesek, de mivel a réseknél a fázisok azonosak, B-re is helyesnek kell lenniük; ezért a B hullámának is meg kell jelennie, mégpedig rekonstruáltan.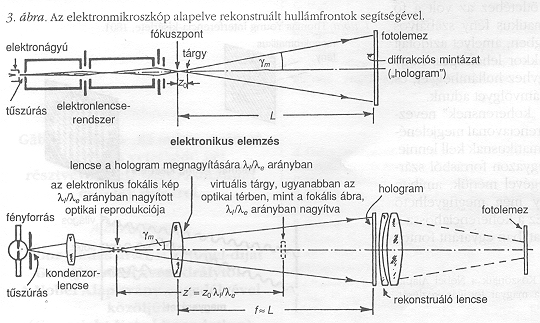

Egy kis matematika hamarosan megmutatta, hogy az elv egynél több tárgypontra, vagyis bármely összetett tárgyra is helyes. Később kiderült, hogy a Természet a holográfiában a feltaláló oldalán áll; nem kell éles pozitív képet készítenünk, szinte bármilyen negatívot vehetünk. Ez felbátorított arra, hogy befejezzem rekonstruált-hullámfront elektronmikroszkópos terveimet, ahogy azt később neveztem, és javasoljam a 3. ábrán látható kétlépéses eljárást. Az elektronmikroszkóp arra kellett, hogy interferenciaképet hozzon létre a tárgyhullám és a koherens háttér (azaz a megvilágító hullám nem-diffraktált része) között. Ezt az interferenciaképet “hologramnak" neveztem, a “holos", “teljes" görög szóból, mivel az interferenciakép a teljes információt tartalmazza. A hologramot ezután fénnyel rekonstruáltuk, olyan optikai módszerrel, ami korrigálta az elektronoptika aberrációit.

Munkám során két nagy fizikus, W.L. Bragg és Frits Zernike vállán álltam. Bragg pár évvel korábban mutatta meg nekem “röntgensugár mikroszkópját", egy optikai Fourier-transzformációs eszközt. Ha behelyezzük a reciprokrács kis képét, az elektronsűrűségek vetületét kapjuk, de csak bizonyos kivételes esetekben, ha a fázisok valamennyien valósak és azonos előjelűek. Sem én, sem Bragg nem tudtuk abban az időben, hogy Mieczislav Wolfke 1920-ban már javasolta ezt a módszert, de kísérleti megvalósítás nélkül. A kétlépéses eljárást így Bragg inspirálta. Másrészt a koherens hátteret nagy sikerrel alkalmazta Frits Zernike a lencsetorzításokon végzett gyönyörű vizsgálataiban, nemcsak intenzitásukat, hanem fázisukat is megjelenítve. Csak a rekonstrukciós elvet hagyták ki.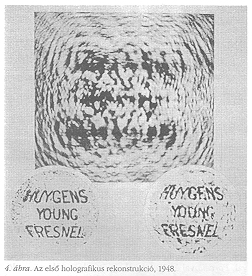

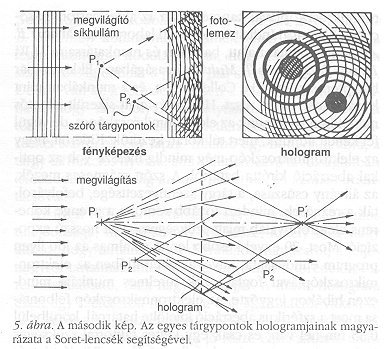
1947-ben Rugbyben, Angliában dolgoztam a British Thomson-Houston Company kísérleti laboratóriumában. Szerencse, hogy a holográfia ötlete az elektronmikroszkópián keresztül jött, mert ha csak optikai holográfiára gondoltam volna, a kutatási igazgató, L.J. Davies, kifogásolhatta volna, hogy a BTH társaság elektronikai cég, és nem foglalkozik optikai kérdésekkel. De mivel testvércégünk, a Metropolitan Vickers készített elektronmikroszkópokat, engedélyt kaptam néhány optikai kísérlet végrehajtására. A 4. ábra egyik első holografikus rekonstrukciónkat mutatja. A kísérletek nem voltak könnyűek. A koherencia és intenzitás közti legjobb kompromisszumot nagynyomású higanylámpa nyújtotta, amelynek koherenciahossza csak 0,1 mm volt, körülbelül 200 interferenciacsíkra elegendő. Térbeli koherencia eléréséhez viszont nekünk (nekem, és asszisztensemnek, Ivor Williamsnek) egyetlen higanyvonallal kellett megvilágítanunk egy 3 m-es tűszúrást. Ez körülbelül 1 cm átmérőjű tárgyak hologramjainak elkészítéséhez elegendő fényt adott. Az 1 mm átmérőjű mikrofotók néhány perces expozíciókkal készültek az akkoriban elérhető legérzékenyebb emulzióra. A kis koherenciahossz arra kényszerített, hogy mindent egy tengelyen helyezzünk el. Ez a vonalmenti holográfia volt abban az időben az egyetlen lehetséges eljárás. Távolról sem volt még tökéletes. A véletlen zavarokat okozó zajtól eltekintve a képeken szisztematikus hiba volt, amint az a betűk torzulásából látható. A magyarázatot az 5. ábra adja meg. A zavar abból a tényből ered, hogy nem egy kép van, hanem kettő. A tárgy minden pontja szekundér gömbhullámot bocsát ki, amely interferál a háttérrel, így Fresnel-zónák cirkuláris rendszerét hozza létre. E rendszer Soret-lencseként ismert az optikus után, aki először állított elő ilyet. Ez egyidejűleg pozitív és negatív lencse. Fókuszainak egyike a tárgypont eredeti helyzetében van, a másik a megvilágító hullámfronthoz képest hozzá konjugált helyzetben. Ha “in-line holográfiát" használunk, mindkét kép a vonalban van, és csak fókuszálással különíthetők el. A szeparáció azonban sohasem teljesen tökéletes, mert szabályos, koherens megvilágításnál minden pont hosszú távolságra elnyúló “nyomdokvizet" hagy maga után.

Később fogom elmondani, hogy a modern lézerholográfia milyen könnyedén siklott át e nehézségen, felhasználva a lézerfény nagyobb koherenciáját, ami viszont 1948-ban még nem állt rendelkezésre. Bíztam azonban abban, hogy ki tudom küszöbölni a második képet abban az célkitűzésben, ami akkoriban különösképpen érdekelt: elektronmikroszkóppal meglátni az atomokat. Ez a módszer, amit a 6. ábra illusztrál, épp az elektronlencsék hibáját, a szférikus aberrációt használta ki, hogy kioltsa a második képet. Ha elektronhologramot készítünk olyan lencsével, amelynek szférikus aberrációja van, majd a két kép egyikét megfelelő optikával korrigáljuk, a másik torzulása kétszeres lesz, ami majdnem teljesen elhalványítja. A 6. ábra mutatja, hogy szinte tökéletesen éles rekonstrukció, amelyben jóformán semmi sem marad a második kép okozta zavarból, nyerhető egy olyan rossz lencsével, amelynek képélessége legalább 10-szer rosszabb, mint az elérni kívánt felbontóképesség. Ilyenfajta rossz lencseként egy rosszul gömbölyített mikroszkóp tárgylencsét használtunk, és a rekonstrukciónál ismételten ezt alkalmaztuk.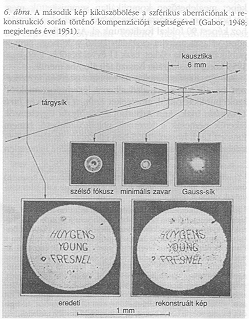

Némi önbizalommal tehát, két évvel később, 1950-ben, megkezdtünk egy programot a holografikus elektronmikroszkópiával kapcsolatban az aldermastoni Associated Electrical Industries kísérleti laboratóriumában T.E. Allibone irányítása alatt, barátaim és munkatársaim M.W. Haine, J. Dyson és T. Mulvey társaságában¹. Ekkorra már beléptem az Imperial Collegiumba, és a munkában mint konzultáns vettem részt. Három év alatt sikerült jelentős mértékben javítanunk az elektronmikroszkópot, de végül fel kellett adnunk, mert túl korán kezdtük. Kiderült, hogy az elektronmikroszkóp még mindig messze volt az optikai aberráció kirótta határtól. A szórt mágneses mezők, az állvány csúszása, a tárgy szennyezettsége, befolyásolták a rezgések, mindezt tovább rontotta a gyenge koherens elektronnyaláb miatt szükségessé vált hosszú expozíció. Most, 20 évvel később lenne alkalmas az idő ilyen program elindítására, mivel az eltelt időben az elektronmikroszkópiával foglalkozók türelmes munkája mindezen hibákon legyőzte. Az elektronmikroszkóp felbontása most a szférikus aberráció kijelölte határnál, körülbelül 0,35 nm-nél van, és csak egy kettes faktorral szükséges javítanunk az atomrácsok felbontásához. Ráadásul már nincs szükség olyan hosszú expozíciókra, mint 1951-ben, mivel a téremissziós katód fejlődése következtében a koherens áram 3-4 nagyságrenddel megnőtt. Talán mégis megérhetem régi ötleteim megvalósulását.

A hullámfront-rekonstrukcióról szóló első cikkeim azonnali válaszokat váltottak ki. G.L. Rogers Angliában jelentősen hozzájárult a technikához, egyebek közt megalkotta az első fázishologramokat, és egyben megvilágította az elméletet. Kaliforniában Alberto Baez, Hussein El-Sum és P. Kirckpatrick figyelemreméltó kísérleteket végzett a röntgenholográfia területén. Részemről munkatársammal, W.P. Goss-szal, konstruáltam egy holografikus interferenciamikroszkópot, amelyben a második képet meglehetősen komplikáltan semmisítettük meg, két hologram egymásra helyezésével, amelyeket egymáshoz képest 90 fokkal fordítottunk el. Az optikai ipar erre adott válasza annyira csalódást keltő volt, hogy nem is publikáltunk róla cikket, csak 11 évvel később, 1966-ban. 1955 körül a holográfia hosszú téli álomba merült.

Az újjászületés hirtelen és robbanásszerűen következett be 1963-ban, az első sikeres lézerhologramokról² szóló publikációkkal, amelyeket Emmett N. Leith és Juris Upatnieks írtak, Ann Arborból a Michigani Egyetemről. Sikerük nemcsak a lézernek volt köszönhető, hanem Emmett Leith hosszú, 1955-ben elkezdett elméleti előkészítésének is. Ez számomra és a világ számára ismeretlen volt, mivel Leith, munkatársaival, Cutronaval, Palermoval, Porcelloval és Viviannal együtt, elgondolásaikat először az oldalra látó radar problémájára alkalmazták, ami abban az időben titkosítva volt. Ez valójában kétdimenziós holográfia elektromágneses hullámokkal, az elektronholográfia egyfajta hasonmása. A radarnál használt elektromágneses hullámok körülbelül 100 000-szer hosszabbak, mint a fényhullámok, míg az elektronhullámok körülbelül 100 000-szer rövidebbek. Eredményeik ragyogóak, de időhiány miatt sajnos nem beszélhetek róluk.

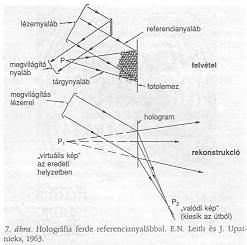
Mikor a lézer 1962-ben elérhetővé vált, Leith és Upatnieks rögtön az enyémeknél sokkal jobb eredményeket produkálhattak, egy új, egyszerű és nagyon hatékony módszert a második kép kiküszöbölésére. Ez a “ferde referencia hullám" módszere, amelyet a 7. ábrán mutatok be. Ezt a hélium-neon lézer nagy koherenciahossza tette lehetővé, ami már 1962-ben körülbelül 3000-szeresen felülmúlta a higanylámpáét. Ez lehetővé tette a referenciahullám elkülönítését a megvilágító hullámtól: ahelyett, hogy keresztülmenne a tárgyon, most megkerülheti. Az eredmény az lett, hogy a két rekonstruált kép nemcsak mélységben, hanem szögben is elkülönült egymástól, a referencianyaláb beesési szögének kétszeresével. A koherens lézerfény intenzitása ráadásul milliószorosan felülmúlta a higanyét. Ez tette lehetővé nagyon finomszemcséjű, alacsony sebességű fotoemulzió használatát és nagy hologramok készítését, ésszerű expozíciós időkkel.

A 8. ábra kettőt mutat Leith és Upatnieks legkorábbi, 1963-ban készített rekonstrukcióiból, amelyek már sokkalta jobbak voltak azoknál, amiket 1948-ban létrehozhattam. E két kép különös érdekessége, hogy ugyanazon hologram rekonstrukciói, a referencianyaláb különböző helyzetében felvéve. Ez volt az első bizonyítéka a hologramok magasabbrendű tárolóképességének. Leith és Upatnieks hamarosan 12 különböző képet tudott tárolni egyetlen emulzióban. Manapság 100, sőt 300 oldalnyi nyomtatott anyag tárolható azon a területen, ami közönséges fotográfiával csak egyre lenne elegendő.

Azóta nagyon felgyorsult a fejlődés. Az első év leglátványosabb eredménye a három dimenziós tárgyak holográfiája volt, ami mindkét szemünk egyidejű használatával látható. A holográfia természetesen kezdettől fogva háromdimenziós volt, de az én korai, kicsi hologramjaimban ez csak a téren keresztüli fókuszálás segítségével, mikroszkóppal vagy rövid gyújtótávolságú szemlencsével volt látható. Ez azonban nem volt elég a hologram megnagyobbításához. Az is szükséges, hogy a fotolemez minden pontja lássa a tárgy minden pontját. A korai, szabályos megvilágítással készült hologramokban az információ kis területen tárolódott, a diffrakciós mintázatban.

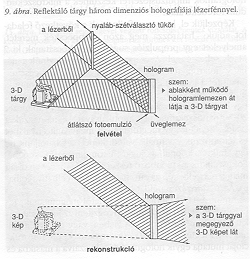
Diffúz tárgyak esetében nem szükséges különleges elővigyázatosság. A felület kis gödröcskéi és kiugrásai egy nagy kúp mentén szórják a fényt. A 9. ábra példát mutat az összeállításra egy érdes tárgy, mint Abraham Lincoln szobrocskája esetében. Elhalványított hologrammal (“fázishologram") az a benyomásunk, hogy egy tiszta ablakon át magára a szobrocskára nézünk.

Ha a tárgy nem fényvisszaverő, például egy diapozitív lemez, az információ az egész hologram területén terjed szét, a tárgyat egy diffúzoron keresztül világítva meg, amilyen például egy zúzmarás üveglap. Egy ilyen “diffúz" hologram külseje rendkívüli: olyan, mintha zaj lenne. “Ideális Shannon-kódolásnak" nevezhetjük, mivel Claude E. Shannon kommunikációelméletében megmutatta: a leghatékonyabb kódolás olyan, hogy látszólag minden szabályosság eltűnik a jelből; “zaj-szerű"-nek kell lennie. De hol van az információ ebben a káoszban? Megmutatható, hogy nem olyan szabálytalan, mint amilyennek tűnik. Nem olyan, mintha véletlenszerűen homokszemcséket szórnánk egy lapra. Inkább egy bonyolult ábra, a tárgy diffrakciós nyoma, ami véletlenszerű távolságokban ismétlődik, de mindig azonos méretben és azonos orientációval.

Az ilyen diffúz hologramok nagyon érdekes és fontos tulajdonsága, hogy bármely kis része, amely elég nagy ahhoz, hogy tartalmazza a diffrakciós mintázatot, a teljes tárgyról tartalmaz információt, ami tehát a töredékből is rekonstruálható, csak nagyobb zajjal. A diffúz hologram ezért egy szétosztott memória. Sok spekulációt váltott ki az a kérdés, hogy az emberi emlékezet is holografikus-e, mivel jól ismert, hogy az agy jó része elpusztítható anélkül, hogy a memória minden nyomát kitörölnénk. Nincs most időnk arra, hogy ezt a nagyon izgalmas kérdést megtárgyaljuk. Csak annyit akarok mondani, hogy szerintem az emberi memóriával való hasonlatosság csak funkcionális, és biztosan nem szerkezeti.

Látható, hogy a holográfia fejlődése során a hologramok a tárgytól egyre különbözőbbé, a rekonstrukciók pedig egyre tökéletesebbé váltak.

Ann Arborban, a Michigani Egyetemen végrehajtott úttörő munka a holografikus technikák stabilizációjához is vezetett. Ma a laboratóriumok százai, ha nem ezrei rendelkeznek ilyen berendezéssel: nagyon stabil gránittábla vagy acélasztal különböző optikai eszközökkel a koherens fény kezeléséhez, amilyet most az optikai ipar gyárt. A nagy stabilitás abszolút lényeges minden, folytonos üzemű lézerrel végzett munkában, mivel az expozíció folyamán történő negyedhullámhossz nagyságrendű elmozdulás teljesen tönkretesz egy hologramot.

1965-től máig azonban kifejlődött a holográfia egy fontos ága, ahol a nagy stabilitás nem szükséges, mivel a hologramok impulzuslézerrel készülnek a mikroszekundum töredéke alatt.

Képzeljük el, hogy egy fizikusnak a következő feladatot adjuk: “határozza meg azon cseppecskék méretét, amelyeket egy propulziós sugárcsőből bocsátanak ki 2 Mach sebességgel. A cseppek mérete valószínűleg néhány mikron felett lesz." Bizonyára kétségbeesetten emeli fel a kezét! Pedig mindössze annyit kell tennünk, hogy megörökítjük a sugár egyszerű vonalhologramját egy biztonságos távolságban levő lemezre, egy rubinlézer 20-30 nanoszekundumos impulzusával. Utána nézzük a “valós" képet (vagy megfordítjuk a megvilágító nyalábot és létrehozzuk a virtuális valódi képét), és hatoljunk be egy mikroszkóppal a sugár háromdimenziós képébe. Fókuszáljunk a különböző részecskékre. A nagy távolság miatt a második kép zavaró hatása teljesen elhanyagolható. A 10. ábra szép példát mutat erre.

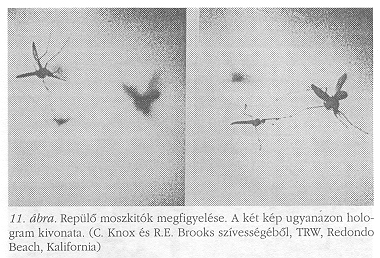
Amint a TRW laboratórium kutatói megmutatták, lehetséges egyetlen hologramban rögzíteni az infuzóriumokat néhány méternyi piszkos vízben, vagy rovarokat egy méternyi légtérben. A 11. ábra rovarok két rekonstrukcióját mutatja egyik hologramból fókuszálva a másikba és így tovább. A szerzők, C. Knox és R.E. Brooks holografikus mozgófilm felvételét is elkészítették, amelyben egy moszkitó röptét követték igen nagy mélységen át, amelyet minden filmkockán újrafókuszáltak.

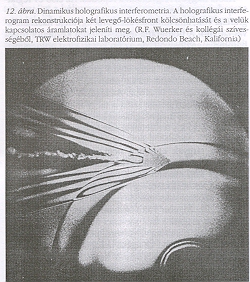
A TRW csoport, Ralph Wuerker és kollégái, egyik fontos eredménye a holográfia egy másik ágához vezet, a holografikus interferometriához. A 12. ábra egy lövedék rekonstrukcióját mutatja, lökéshullámainak vonulatával együtt, amint az találkozik egy másik lökéshullámmal. De ez nem csak egy egyszerű kép, ez interferometrikus kép. A csíkok mutatják azokat a helyeket, amelyeknél a fény lemaradása egész hullámhossznyi, az esemény előtti nyugvó levegőhöz képest. A viszonyítási alapot előzetes expozícióval kapták. Ez tehát kettős-exponálású hologram, amelyről később részletesebben szólok.

Az impulzus holográfia egy másik jelentős fejleménye: a holografikus, háromdimenziós portré. Ez a lézerfejlesztésben történt kiemelkedő munka eredménye. A rubinlézer, amint először T.H. Maiman megvalósította, képes volt rövid impulzusokra, de koherenciahossza csak néhány centiméteres nagyságrendű volt. Ez nem akadály a vonalmenti holográfia esetében, ahol a referenciahullám úgy terjed, hogy szinte lépést tart a diffraktált hullámocskákkal, de egy, mondjuk méternyi mélységű helyszínen levő reflektáló tárgyak felvétele céljából legalább egy méteres koherenciahossz szükséges. Manapság elérhetőek 30 nanoszekundum időtartamú egy-módusú impulzusok 10 joule nyalábenergiával és 5-8 méter koherenciahosszal. Ilyeneket használtunk saját holografikus portrém felvételéhez, amelyet az előadásomhoz kapcsolódó kiállításon mutatunk be.

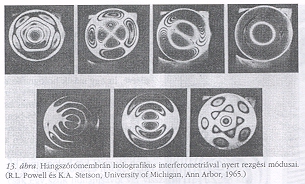
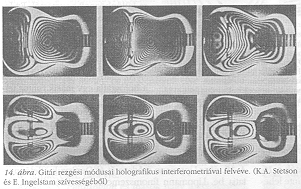
1965-ben Ann Arborban, a Michigani Egyetemen, R.L. Powell és K.A. Stetson érdekes felfedezést tett: a mozgó tárgyak holografikus képei elmosódnak. Ha azonban kettős expozíciót használunk, először a nyugvó, aztán a rezgő tárgy esetében, csíkok jelennek meg, jelezvén azokat a vonalakat, ahol az elmozdulás a félhullámhossz többszörösét teszi ki. A 13. ábra egy hangszórómembrán rezgési módusait mutatja, ahogy Powell és Stetson vette fel 1965-ben. A 14. ábrán látható ugyanez egy gitárral kapcsolatban, amelyet K.A. Stetson készített Erik Ingelstam laboratóriumában.

Különös módon, a TRW csoport interferogramjai, valamint Powell és Stetson vibrációs felvételei egyaránt az interferometrikus elv egyszerűbb alkalmazását példázzák, aminek történetileg előbb kellene jönnie - ha a tudomány haladása mindig a legrövidebb utat követné. Ez nem más, mint a szilárd testek kis deformációinak megfigyelése kettős expozíciójú hologramok segítségével. Az egyszerű magyarázat a következő: vesszük egy test hologramját az A állapotban. Ez azt jelenti, hogy a referencianyaláb segítségével befagyasztjuk az A hullámot. Ezután deformáljuk a testet úgy, hogy az vegye fel a B állapotot, majd felveszünk egy második hologramot ugyanarra az emulzióra, ugyanazzal a referencianyalábbal. Előhívjuk a hologramot, és megvilágítjuk a referencianyalábbal. Most a két hullám, A és B, amelyeket különböző időkben fagyasztottunk be, és amelyek sohasem találkoztak, egyidejűleg jönnek elő, és interferálnak egymással. Az eredmény az, hogy Newton-gyűrűk jelennek meg a tárgyon, és mindegyik csík félhullámhossznyi deformációnak felel meg. Az elvet egyidejűleg és egymástól függetlenül fedezte fel J.M. Burch Angliában, valamint G.W. Stroke és A. Labeyrie a michigani Ann Arborban.

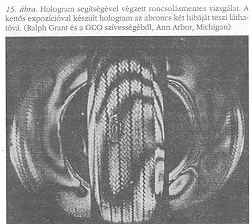
A holografikus interferometriával történő roncsolásmentes vizsgálat jelenleg a holográfia messze legfontosabb ipari alkalmazása. Nagyban hozzájárult az első, holográfián alapuló cég, a GCO (G.C. Optronics) létrejöttéhez a michigani Ann Arborban. A következő példákat a GCO szívességéből mutatjuk be. A 15. ábrán egy autóabroncs ellenőrzését látjuk. Az abroncs elejét közvetlenül holografálták, az oldalak két tükörben láthatók jobb- és baloldalt. Először kis idő szükséges az abroncs megállapodásához, majd felveszik az első hologramot. Ezután kevés forró levegőt fújnak rá, és másodszor is exponálnak ugyanarra a lemezre. Ha az abroncs tökéletes, csak néhány szélesen elhelyezkedő csík tűnik fel, szinte egyenletes tágulást jelezve. Ahol viszont a gumilemezek ragasztása tökéletlen, kis hólyag jelenik meg, amint ez középtájon és a bal felső sarokhoz közel látszik. Az eltérés csak pár ezred milliméter, de olyan hibát jelez, ami komollyá válhat. Az eredmény ugyanaz, ha az első hologramot előhívják, pontosan az eredeti pozícióba helyezik, és az abroncs kitágulását “élőben" figyelik meg.

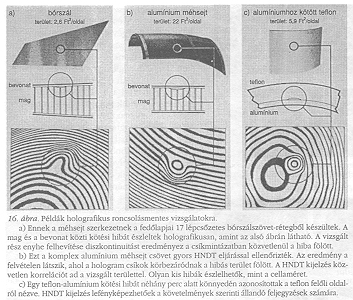
A roncsolásmentes vizsgálat más példái láthatók a 16. ábrán; minden hiba, amelyet lehetetlen vagy szinte lehetetlen más módszerrel észlelni, eltéveszthetetlenül szem elé kerül. A méhsejtszerkezeteket vizsgáló holografikus analizátorral (amint ez a 16. ábra közepén, a repülőgépszárnynál látszik) az alumíniumlemezek és a méhsejt közti legkisebb hegesztési hiba egyetlen pillantással biztonsággal észlelhető.

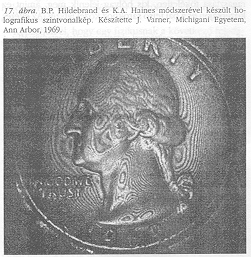
A holografikus interferometria a maga 1/4000 mm csíkegységével tökéletesen alkalmas nagyon kis deformációk észlelésére, ugyanakkor túl érzékeny munkadarabok pontosságának ellenőrzésére. Itt egy másik holografikus technika, a “szintvonalazás" a megfelelő. Ezt először Haines és Hillebrand alkalmazta 1965-ben, legújabban pedig J. Varner jelentősen továbbfejlesztette, szintén a michigani Ann Arborban. Ugyanazon tárgyról két hologramot készítünk, de két hullámhosszal, amelyek például egy százaléknyira különböznek egymástól. Ez lebegést eredményez a két csíkrendszer között, körülbelül 1/40 mm csíktávolsággal, ami pontosan az, amire a műhelynek szüksége van (17. ábra).

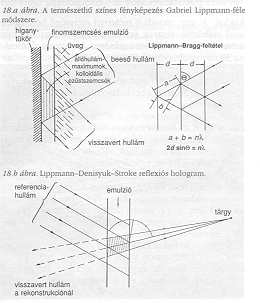
Az ipari alkalmazásoktól most a holográfia egy másik fontos fejlődéséhez fordulok. 1962-ben, éppen a “holográfia robbanás" előtt, Yu.N. Denisyuk szovjet fizikus publikált egy fontos cikket, amelyben a holográfiát a természetes színekkel való fényképezés zseniális módszerével kombinálta, amelyért Gabriel Lippmann 1908-ban Nobel-díjat kapott. A 18. ábra Lippmann módszerét és Denisyuk ötletét mutatja be. Lippmann finomszemcsés emulziót állított elő kollodiális ezüstbromiddal, és az emulziót tükörként szolgáló higany hátréteggel látta el. Az emulzióra eső fény visszaverődik a tükrön, és állóhullámokat képez. Az elektromos térerősség maximumainál kolloidális ezüstszemcsék precipitálódnak azon rétegekben, amelyek jó közelítéssel félhullámhossznyira helyezkednek el. Előhívás után az összes réteget fehér fénnyel megvilágítva, csak egy szűk hullámsávot ver vissza az eredeti szín körül, mivel a Lippmann-rétegeken szórt hullámocskák csak erre a színre adódnak össze fázisban.

Denisyuk javaslata a második diagramon látható. A tárgyhullám és a referenciahullám az emulzió ellentétes oldalairól esik be. Újra állóhullámok és Lippmann-rétegek képződnek, de ezek többé nem párhuzamosak az emulzió felületével, hanem felezik a két hullámfront közti szöget. Ha most - és ez Denisyuk elve - az előhívott emulziót a referenciahullámmal megvilágítják, a tárgy az eredeti pozícióban és (hacsak az emulzió össze nem zsugorodik) az eredeti színben jelenik meg.

Noha Denisyuk figyelemreméltó kísérleti készséget árult el, 1962-ben lézer hiányában csak “létezésbizonyítékot" produkálhatott. Kétszínű, fehér fénnyel megvilágítható reflexiós hologramot először 1965-ben készített G.W. Stroke és A. Labeyre.

Azóta K.S. Pennington és mások nagy tökéletességű, egyszínű reflexiós hologramokat fejlesztettek ki új fotografikus eljárásokkal, 100%-ot közelítő reflexióval. De a két- és méginkább a háromszínű hologramok még mindig távol vannak a tökéletestől: Jelenleg fő gondjaim egyike, hogy javítsak a helyzeten, de túl sokáig tartana és még nagyon korai is lenne beszélni róla.

A holográfia egyik alkalmazása, ami bizonyára nagy fontosságra tesz szert a következő években, az információtárolás. Korábban említettem, hogy a holográfia 100-300-szor annyi nyomtatott oldal tárolását teszi lehetővé egy adott emulzión mint közönséges mikrofényképen. Még a mélységi dimenzió alkalmazása nélkül is az arány jobb, mint 50. Az ok az, hogy egy diffúz hologram majdnem ideális kódolást valósít meg, a terület és az emulzió gradációjának teljes kihasználásával, míg a nyomtatott anyag a területnek csak 5-10%-át használja, és a gradációt egyáltalán nem. Egy további faktor a harmadik dimenzióból, az emulzió mélységének kihasználásából ered. Erre a lehetőségre először P.J. van Heerden mutatott rá zseniális cikkében, 1963-ban. Elméletileg lehetségesnek tűnik, hogy egy bit információt tároljunk egy hullámhossznyi kockában. Ez távol áll a megvalósulástól, de a korábban említett 300-as szám teljesen reális.

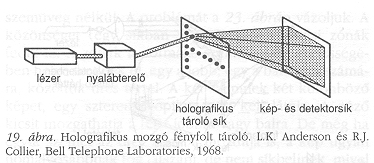
A holografikus tárolás azonban még e hatalmas faktor nélkül is fontos előnyöket kínál. A bináris tárolás ostáblamintázat formájában mikrofilmen egyetlen porszemmel, egy hajszállal vagy egy karcolással tönkretehető, míg egy diffúz hologram ilyen hibákra szinte érzéketlen. Amint azt a 19. ábra illusztrálja, a holografikus tárolás szerzője, L.K. Anderson szerint (1968) ez csak egy szerény kezdet, mégis képes elérni például 64 x 64 nyomtatott oldal bármelyikét körülbelül egy mikroszekundum alatt. Mindegyik 1,2 mm átmérőjű hologram körülbelül 10~ bitet tartalmazhat. Ezen információ egymás utáni kiolvasása egy mikroszekundum alatt természetesen egy lehetetlen hullámsávot követelne meg, de hatásos párhuzamos olvasó eszközök elérhetőek. Bizalommal várhatjuk e “szerény kezdet" elterjedését, mihelyt az adatbank-programhoz komolyan nekilátnak.

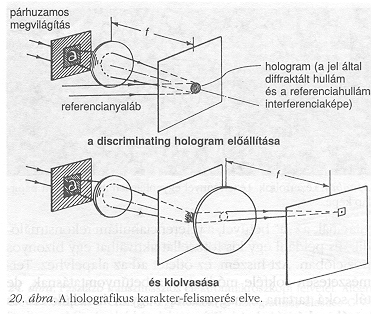
A holográfia egy másik alkalmazása, ami valószínűleg csak korai stádiumban van, az ábra- és karakterfelismerés. Csak röviden utalhatok az alapmunkára, amit A. Vander Lugt végzett a mintázatfelismerés területén. Itt elegendő lesz a karakterfelismerés alapelveit megmagyarázni a 20. ábra segítségével.

Kicsit általánosítsuk a holográfia alapelveit. Minden korábbi példánál egy összetett tárgyhullám interferált egy egyszerű vagy szférikus referencianyalábbal, és a tárgyhullámot úgy rekonstruáltuk, hogy megvilágítsa a hologramot a referencianyalábbal. De egy kis matematika megmutatja, hogy ez bármely referenciahullámra kiterjeszthető, amely élesen korrelál sajátmagával. Az autokorrelációs függvény egy nyaláb invariánsa, és bármely keresztmetszetben kiszámítható. Rögtön látszik, hogy egy gömbhullám élesen korrelál sajátmagával, mivel egy “pontból" bocsátjuk ki. De más nyalábok is vannak, amelyek élesen korrelálnak saját magukkal, például azok, amelyek egy ujjlenyomatból vagy egy kínai írásjelből származnak. Extrém esetben azok is, amelyek egy zúzmarás üvegdarabból erednek. Ezért teljességgel lehetséges például, hogy egy hologram segítségével egy kínai írásjelet a megfelelő angol mondatra fordítsunk és vica versa. J.N. Butters és M. Wall a Loughborough Egyetemen újabban olyan hologramokat készített, amelyek egy portréból létrehozzák a tulajdonos aláírását, és fordítva. Más szavakkal, egy hologram univerzális fordító lehet. Például lefordíthat egy általunk olvasható jelet egy másikra, amit egy gép olvashat.

A 20. ábra ennek az elvnek egy egészen szerény megvalósítását mutatja. Egy “a" betű hologramja készült sík referenciahullám segítségével. Ha ezt a hologramot megvilágítják az “a" betűvel, a referenciahullám rekonstruálódik, és például egy kis fotocellát aktiválhat egy bizonyos pozícióban. Azt hiszem, ez ötletet ad az alapelvhez. Természetesen sokféle módja van a betűnyomtatásnak, de túl soká tartana elmagyarázni, hogyan kezeljük ezt és egyéb nehézségeket.

A karakterfelismerő eszközökkel már egy fél lépést tettünk a jövőbe, mivel ezek valószínűleg csak a számítógépek és robotok következő generációjában válnak fontossá, amelyeknek kicsivel több emberi intelligenciát kell adnunk. Most röviden meg szeretnék említeni néhány további problémát, amelyek félig, vagy több mint félig még csak a jövőben léteznek.

Az egyik, ami már nagyon aktuális, a lézerfoltok legyőzése. Mindenki, aki lézerfényt lát, először meglepődik a simának látszó tárgy érdes megjelenésén. Egy fehér papírlap olyannak tűnik, mintha hangyák nyüzsögnének rajta. A nyüzsgést a szem nyugtalansága okozza, de a felület érdessége valódi. Ezt nevezik “lézerfolt"-nak, amelyre a 21. ábra mutat jellegzetes példát. Egy fehér papírlapnak ilyen a megjelenése lézerfényben, amikor egy alacsony teljesítményű optikai rendszerrel nézzük. Ez nem valódi zaj, hanem olyan információ, amit nem akarunk. Információ a papír mikroszkopikus egyenetlenségéről, amire nem vagyunk kíváncsiak. Mit tehetünk ellene?

Érdes tárgyak esetében a válasz sajnos a következő: mindaz, amit tehetünk, hogy nagyobb területre átlagolunk, így simítva el az eltéréseket. Ez azt jelenti, hogy az információ nagy részét félre kell dobnunk, a hasznosat és a nemkívántat egyaránt. Ez sajnálatos, de semmi mást nem tehetünk. Sok esetben van is elegendő információnk, amit félredobhatunk, amint a diffúz hologramokból eredő, itt bemutatott rekonstrukciók némelyikének teljesen kielégítő megjelenéséből látható. Vannak azonban fontos területek, amelyeken sokkal többet tehetünk, és ahol az előrehaladásra nagyon is szükségünk van. Ez a mikrohologramok tárolásának és megjelenítésének területe. Ezek diffúz hologramként készülnek, abból a célból, hogy biztosítsuk a portól és karcolásoktól való mentességet, de diffúzzá tételükkel foltokat viszünk be, és ennek elkerülésére az ilyen hologramok manapság sokkal nagyobbra készülnek, mint az ideálisan szükséges lenne. Mostanában mutattam meg, hogy a diffúz hologramok előnyei majdnem teljesen megőrizhetőek, míg a foltosság, speciális megvilágító rendszert használva fagyott üveg helyett, teljesen kiküszöbölhető. Remélem, ez további haladást eredményez a holografikus tárolók információsűrűségében.

Tegyünk most egy radikálisabb lépést a jövőbe. Röviden szeretném megemlíteni két kedvenc holografikus agyszüleményemet. Az első a Panorámikus Holográfia, amit másképpen Holografikus Művészetnek is hívhatunk.

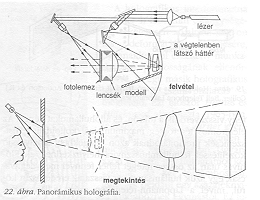
Minden eddig készített háromdimenziós hologram csupán néhány méter mélységre terjed ki. Nem lehetne a végtelenbe tágítani? Nem tehetnénk egy olyan hologramot a falra, ami ablak benyomását kelti, amelyen keresztül egy valódi vagy elképzelt tájképet láthatunk? Azt hiszem, meg lehet csinálni, de ez nem fénykép lenne, hanem műalkotás. A 22. ábra illusztrálja az eljárást. A művész készít egy modellt, olymódon torzítva, hogy perspektivikusnak és bármely távolságra kiterjedőnek látszódjék, ha egy olyan nagy lencsén át nézzük, mint a hologram. A művész használhat kisebb lencsét is, de elég nagyot ahhoz, hogy mindkét szemét befedje, mikor a modellt készíti. A modellről reflexiós hologram készül egy erős, kisméretű fényforrással. A szemlélő azt látja, amit a lemez látott a lencsén keresztül; vagyis egy természetes színű, tetszőleges távolságra kiterjedő tájképet. A terv fejlesztés alatt áll, de még igen sokat kell dolgoznunk rajta, hogy kielégítővé legyen, mivel először nagy mértékben fokoznunk kell , a háromszínű hologramok reflexióképességét.

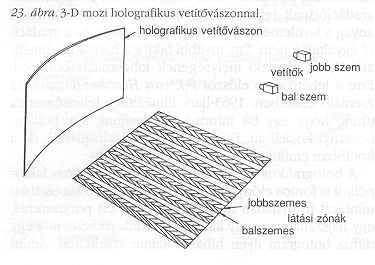
Egy még ambiciózusabb terv, valószínűleg a még távolabbi jövőben, a háromdimenziós mozgókép-fényképezés, speciális segédeszköz, mint például polaroid szemüveg nélkül. A problémát a 23. ábrán vázoljuk. A közönséget (egy síkban vagy kettőben) látási zónák fedik le. A zónák a normális szemtávolság szélességében helyezkednek el, egy a jobb, egy a bal szem számára, közöttük üres térrel. A két szemnek két különböző képet, egy sztereoszkopikus párt kell látnia. A néző kicsit mozgathatja a fejét jobbra vagy balra. De még ha egyik szemét az üres zónába mozdítja is, a kép ugyan homályosabbnak fog látszani, de nem síkbelinek, mivel az egyik szem is képes az “alapbeállításban" a sztereoszkópia benyomását kelteni.

Több évig dolgoztam ezen a problémán, épp a holográfia előtt, amíg be kellet látnom, hogy az optika hagyományos eszközeivel, a lencsékkel, tükrökkel és prizmákkal ez teljességgel megoldhatatlan. Kielégítően kis mozivásznakat készíthetünk kis filmszínházak számára, de nagy mozivásznakkal és nagy filmszínházakkal dilemmába kerülünk. Ha a lencsék vagy ilyesmik nagyok, az első ülésekből láthatók lesznek; ha kicsik, a hátsó sorokban nem lesz megfelelő a képélesség.

Néhány éve meglepődve jöttem rá, hogy a holográfia ezt a problémát is meg tudja oldani. Használjunk egy vetítőt úgy, mint referenciaforrást, és például a bal látó zónák rendszerét, mint tárgyat. A Lippmann-emulzióval fedett mozivászon automatikusan egy nagyon komplikált optikai rendszerré alakul, olyanná, hogy amikor a képet vetítik, csak a bal látási zónákból lesz látható. Utána megismételjük az eljárást a jobb vetítővel és a jobb látási zónákkal. A háromdimenziós (Lippmann-Denisyuk) hologramok megjelenítik a vételiránytól függő szelektivitás jelenségét. Ha a megvilágítót az eredeti helyzetéből bizonyos szöggel elmozdítjuk, nem lesz reflexió. A két vetítőt ebben a szögben helyezzük el egymástól (vagy kicsit nagyobb szögben), aminek hatására a jobb kép nem lesz látható bal szemmel és fordítva.

Természetesen marad egy probléma. Az, hogy nem tudunk filmszínház-mérete holográfiát alkalmazni olyan nagy fényképező lemezzel, mint a mozivászon. De ez is megoldható, ha a mozivásznat kis darabokból állítjuk össze, nem a színházban, hanem a színház modelljében, amit aztán lencsén át nézünk, és ami így egészen hasonló a panorámikus holográfiában használatoshoz.

Remélem, érzékeltettem a terv megvalósíthatóságát, de érzékeltettem a nehézségeit is. Abban viszont nem vagyok biztos, hogy ezek le is győzhetőek a 20. században, vagy akár a következőben.

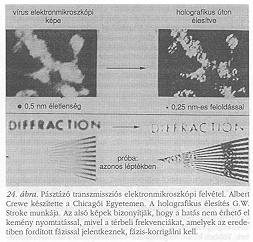
Ambiciózus tervek, amelyekre veleszületett hajlamom van, és amelyek megvalósítása hosszú időt vesz igénybe. Mint az elején mondtam, szerencsés leszek, ha még megérem a holografikus elektronmikroszkópia megvalósulását, amellyel 24 éve kezdtem el foglalkozni. De reménykedem, mert nagy mértékben felbátorított G.W. Stroke figyelemreméltó eredménye, amelyet a 24. ábra mutat be. Stroke-nak sikerült csökkenteni a pásztázó transzmissziós elektronmikroszkópon felvett mikrofényképek elmosódottságát egy holografikus szűrő eljárással, a képfelbontást ezzel 0,5 nm-ről körülbelül 0,25 nm-re javította. A felvételeket a chicagói Albert Crewe készítette. Ez tulajdonképpen nem holografikus elektronmikroszkópia; mivel az eredetit nem koherens elektronokkal vették fel. de a A. Crewe és G.W. Stroke által használt technikák olyan hatékonyak, hogy bízom benne, sikeresek lesznek a következő, sokkal nagyobb és fontosabb lépésben is.

Összegezve, azon kevés szerencsés fizikus egyike vagyok, akik láthatják, amint egyik ötletük a fizika kiterjedt fejezetévé fejlődik. Mélységes meggyőződésem, hogy ezt egy fiatal, tehetséges és lelkes kutatókból álló csapat érte el, akik közül csak néhány nevet említhettem. Szívbéli köszönetemet akarom kifejezni nekik, amiért munkájukkal hozzásegítettek engem a legnagyobb tudományos elismeréshez.

________________________

1 Támogatva a D.S.I.R. (Direction of Scientific and Industrial Research) ösztöndíjával, az első ösztöndíj, amit ez a testület egy ipari laboratóriumnak valaha is adott.

2 Többször megkérdeztek, hogy miért nem én fedeztem fel a lézert. Tulajdonképpen gondoltam rá. 1950-ben a koherens fény erős sugárzásának szükségességére gondolva, visszaemlékeztem, hogy 1921-ben Berlinben, mint fiatal egyetemi hallgató, magától Einsteintől hallottam a Planck-törvény csodálatos levezetését, amely az indukált emissziók létezését posztulálta. Ezután nekem volt egy ötletem az impulzuslézerrel kapcsolatban: vegyünk egy megfelelő kristályt, készítsük el ennek rezonátorát egy erősen visszatükröző bevonattal, töltsük tele a felső szintig, megvilágítván egy kicsi lyukon keresztül, és süssük ki robbanásszerűen saját fényének egy sugarával. Legjobb tanítványomnak ajánlottam ezt mint doktori témát, de ő visszautasította, mint túl kockázatosat. Mi tagadás, én sem voltam biztos benne, hogy megfelelő kristályt találnánk.

________________________

Copyright: Nobel Alapítvány, Stockholm. Köszönjük a Nobel Alapítványnak, hogy engedélyezte lapunknak a magyar fordítás közlését. Fordította Tárczy Szilvia és Zsolt Gábor