KONTAKT KETTÔSCSILLAGOK FIZIKAI PARAMÉTEREINEK MEGHATÁROZÁSA
Tartalomjegyzék
Bevezetés
Fedési kettôscsillagok
A kettôscsillagok és a fedési kettôsök osztályozása
W UMa típusú csillagok
Periódusváltozás kettôs rendszerekben
Mûszertechnikai áttekintés
Mûszertechnikai összefoglaló
A csillagok kiválasztása
Az AW Ursae Majoris és az FU Dra fizikai paramétereinek meghatározása
AW UMa
I. Irodalmi feldolgozás
II. Periódusváltozás vizsgálata
III. Fizikai paraméterek meghatározása
FU Dra
I. Képeim feldolgozása, kiértékelése
II. Perióduskorrekció
III. Radiális sebességek
Fénygörbemodellezés
A NIGHTFALL program
A program tesztelése
Az FU Dra fénygörbe-modellezése
Az FU Dra fizikai paramétereinek meghatározása
Összefoglalás
I. AW UMa érintkezô kettôscsillag
II. FU Dra érintkezô kettôscsillag
Köszönetnyilvánítás
Irodalomjegyzék
Bevezetés
David Fabricius (1564–1617) amatôr csillagász 1596-ban felfigyelt egy fényes csillagra a Cet csillagképben, aminek a fénye néhány hét alatt fokozatosan gyengült, míg végül teljesen eltûnt szem elôl. 1638-ban Holwarda megfigyeléseket végzett ugyanazon csillagról, és azt tapasztalta, hogy a csillag változtatja a fényességét. E különös csillag Mira (csodálatos) néven vált ismertté. Majdnem 150 éves csönd után Figott és Goodricke 5-6 változó fényû csillagot fedezett fel. 1865-ben már 113 változóig jutott el a számuk. A századforduló elôtt a fotografikus keresés felgyorsította az eseményeket, majd az 1980-as évtôl a különbözô programok, mûholdak megsokszorozták a változócsillagok számát. Ma már több százezerre gyarapodott a számuk.
A változás az, ami árulkodik a fejlôdésrôl, a lejátszódó folyamatokról - nemcsak az embernél, hanem a csillagoknál is. Hogy megértsük, miért változik egy csillag, ahhoz pontosan nyomon kell követnünk, hogyan változik. Azt a grafikont, ami megmutatja, hogyan változik egy csillag fényessége az idôben, fénygörbének nevezzük, melynek megrajzolásához rendszeresen mérnünk kell.
Jelen dolgozat a változócsillagok népes csoportjából két fedési kettôscsillag, az AW Ursae Majoris és az FU Draconis irodalmi feldolgozását, illetve az utóbbi rendszer mérését és annak feldolgozását mutatja be. Az AW UMa régóta ismert fedési kettôs, melynek pontosítottam a periódusát, és meghatároztam a fizikai paramétereit. Az FU Dra-t a Hipparcos mûhold fedezte fel nemrégiben. E rendszer fényváltozását CCD-fotometria segítségével mértem meg. A méréseket Baján végeztem, 2000. június 26. és június 30. között. Három éjszaka alatt 645 képet készítettem. Saját megfigyeléseimbôl megállapítottam, hogy a rendszer ún. teljes fedést mutat. További paraméterek meghatározásához egy fedési fénygörbe-modellezô programot használtam, melyet a régóta ismert kettôs modellezésével teszteltem, mielôtt alkalmaztam volna a kevésbé ismert rendszerre.
Hogy elkerüljem az „in medias res" jellegû kezdést, elôször röviden áttekin-tem a témához kapcsolódó csillagászati ismereteket, majd ismertetném a mérésem mûszertechnikai vonatkozásait (mérôrendszer, mérési módszer, ill. csillagok kiválasztása). Bemutatom a periódus- és paramétermeghatározást, a konkrét méréseket, az adatok feldolgozását. Végül magáról a modellezésrôl, és annak eredményérôl írok.
A kontakt kettôscsillagok olyan szoros rendszerek, melyekben a komponensek a belsô Lagrange-pontban érintkeznek egymással. Ilyen kettôscsillagok gyakran figyelhetôk meg fedési kettôsként, azonban csillagfejlôdési állapotukról eléggé keveset tudunk. A csillagok tömegét közvetlen úton csak kettôscsillagokban lehet mérni. Emellett a csillag fejlôdését a tömege határozza meg. Célom az volt, hogy a kontakt kettôscsillagok fejlôdési állapotának tanulmányozásához közvetlenül felhasználható eredményeket szolgáltassak a vizsgált rendszerek tömegérôl.
Fedési kettôscsillagok
A kettôscsillagok és a fedési kettôsök osztályozása
A hosszú-hosszú évek során végzett megfigyelések alapján a csillagok több mint felérôl kiderült, hogy van kísérôje, és a rendszert alkotó csillagok a gravitációs vonzás miatt egymás körül keringenek. A kettôscsillagok legkézenfekvôbb csoportosítása a detektálhatóság alapján történô osztályozás:
Vizuális kettôsök: a komponensek külön megfigyelhetôek, és a pályamenti mozgás is kimutatható egyes esetekben.
Spektroszkópiai kettôsök: a színképvonalak periódikus Doppler-eltolódást mutatnak a keringés miatt fellépô radiális sebességváltozás következtében.
Spektrum-kettôsök: különbözô csillagokra jellemzô jegyeket mutat a spektrum; nyilvánvalóan két egymáshoz közeli csillag együttes mérésébôl származik.
Asztrometriai kettôsök: csak az egyik komponens figyelhetô meg, de a csillag látszólagos mozgása egy nem látható kísérô jelenlétét igazolja.
Ellipszoidális kettôsök: tényleges fedés nem figyelhetô meg a pályasík kis hajlásszöge miatt, de az objektumok nem egyenletes fényességeloszlása és torzult alakja a keringés során kis amplitudójú fényességváltozást okoz.
O-C kettôsök: a komponensek közül legalább az egyik periódikus jelforrás - a kisugárzott jel periódusa modulálódik a Doppler-eltolódás következtében.
Fedési kettôsök:olyan kettôscsillagok, melyeknél a komponensek a keringés során a Földrôl nézve idôrôl-idôre elfedik egymást, így a rendszer jellegzetes fényváltozást mutat.A fedéseket vizsgálva az inklináció nagyságától függôen elkülöníthetünk részleges fedést (partial eclipse), ekkor r1–r2>cos i (a kis csillag egy része mindig látszódik), teljes fedést (total eclipse), ekkor r1–r2=cos i, illetve gyûrûs fedést (annular eclipse), ekkor r1–r2<cos i. Itt r1 és r2 a komponensek sugarai, i pedig az inklináció – azaz a rendszer pályasíkja és a megfigyelô között bezárt szög.
A fedési kettôsöket a fénygörbe alakja szerint is osztályozhatjuk. A Változócsillagok Általános Katalógusában (GCVS-ben) is használt klasszifikációs osztályozás a következô:
· Algol-típus (EA): Mély fôminimum, sekély mellékminimum jellemzi, valamint fontos, hogy a fedésen kívüli szakasz fényváltozása közel konstansnak tekinthetô. A fedések kezdete ugrásszerû. A színindex változik a fedés alatt (fedések közben a fôminimum környékén vörösödik, a mellékminimumnál kékül, közötte pedig konstans). Tipikus képviselô: b Persei (Algol).
· b Lyrae-típus (EB): A minimumok mélysége különbözô, a fényváltozás folyamatos a fedésen kívüli szakaszban is. A fedések kezdete nem állapítható meg egyértelmûen. A színindex a fedésen kívül is változik.
· W UMa-típus (EW): A minimumok mélysége hasonló, a fényváltozás a fedésen kívüli szakaszon is folyamatos. A fedések kezdete nem állapítható meg. A színindex nem, vagy csak nagyon kicsit változik.
A fénygörbe alakja szerinti osztályozás azonban nem egyértelmû, ha az EA ill. EB típus közti átmenetet vizsgáljuk. Pl.: több típusba is tartozhat a rendszer, mert a fénygörbe optikai tartományban más lehet, mint infravörösben.
Egy másik csoportosítást 1960-ban Z. Kopal javasolt, ami az ún. Roche-térfogat kitöltöttségén alapul. Jelenlegi ismereteink szerint a Roche-modell a szoros kettôscsillagok fotoszférájának alakját kielégítôen képes megadni. Feltesszük, hogy a kettôscsillag gravitációs terét két tömegpont terével lehet közelíteni, és a kettôs rendszer komponensei hidrosztatikai egyensúlyban vannak, azaz a sûrûség és a nyomás az ekvipotenciális felületek mentén állandó. E feltevés alapján a csillagok egyensúlyi alakjának kiszámítása egyenértékû egy ekvipotenciális felület geometriájának meghatározásával. Az ekvipotenciális felületek egy kritikus potenciálértéknél, a belsô Lagrange-pontban összeérnek, mindkét csillag számára egy kritikus térfogatot (Roche-térfogatot) definiálva. A tömegpontokkal való közelítést az indokolja, hogy a csillagokat alkotó anyag túlnyomó része a centrumhoz közeli, gömbszimmetrikus tartományba sûrûsödik (centrális kondenzáció).
Ezek alapján a Roche-térfogaton alapuló osztályozás a következô:
- Szétválasztott rendszer (detached): mindkét csillag belül van a Roche-térfogatán.
- Félig érintkezô rendszer (semi detached): csak az egyik komponens tölti ki a Roche-üregét – általában a kisebb tömegû.
- Érintkezô rendszer (contact): mindkét csillag kitölti a Roche-térfogatát.
E modell alapján osztályozott rendszerek fontosabb jellemzôi:
- A csillagok viszonylag távol helyezkednek el egymástól, az árapály-erôk gyengék, így a komponensek alakja kicsit tér el a gömbtôl. A pályaperiódus többnyire konstans vagy oszcilláló. Ez utóbbit például apszismozgás, vagy a rendszernek egy harmadik test körüli keringése okozhatja. A pálya gyakran excentrikus, emiatt az ismert apszismozgást mutató rendszerek többsége ebbe az osztályba sorolható (Hegedüs, 1988). Általában fôsorozati vagy fôsorozat elôtti állapotban lévô csillagokat tartalmaz, így a nagyobb méretû komponens nagyobb tömegû és fényesebb.
- A kisebb tömegû komponens szubóriás- vagy óriáscsillag, s kitölti a Roche-üregét. Ezzel ellentétben a nagyobb tömegû fôkomponens korábbi színképtípusú, fôsorozati csillag, s jóval a kritikus térfogaton belül helyezkedik el. Általában a fôkomponens luminozitása a nagyobb. A pályaperiódus növekedése, csökkenése, esetleg fluktuációja figyelhetô meg. A kisebb tömegû csil-lag elôbbre jár a fejlôdésben, ez azonban ellentétben áll a magányos csillagokra érvényes csillagfejlôdési elmélettel (Algol-paradoxon). Ez a komponensek közti tömegátadással magyarázható.
- A W UMa típusú csillagok mind ebbe a csoportba tartoznak. Mindkét csillag kitölti kritikus térfogatát – sôt, néha túl is nônek rajta. A komponen-sek a belsô Lagrange-ponton keresztül érintkeznek, így a hômérsékletük közel azonos. Struktúrájuk és fejlôdési állapotuk jelenleg nem tisztázott. Dolgozatom fô részét képviseli a W UMa-csillagok fizikai paramétereinek vizsgálata, így a következôkben ezen rendszereket mutatom be.
W UMa típusú csillagok
A Nap környezetében végzett statisztikai viszgálatok szerint a W UMa típusú csillagok a kettôscsillagok leggyakrabban elôforduló formái a Galaxisban (Kopal, 1978.). Az ilyen típusba sorolt csillagok megfigyelésébôl adódó tulajdonságai:
- A keringési periódus gyakran erôs változást mutat, értéke általában egy napnál kisebb.
- A komponensek tömegaránya (definíció szerint q=M2/ M1) 1-tôl különbözô értéket vesz fel. A jelenleg ismert szélsôértékek: q= 0,08 (AW UMa), q= 0,88 (SW Lac).
- Színképtípusuk A-típusnál késôbbi, többnyire G- K közötti.
- Luminozitási osztályuk V, tehát kis tömegû, fôsorozathoz közeli objektumok.
- A csillagok tömegét és luminozitását összevetve a mellékkomponens többlet-luminozitást mutat, míg a fôkomponens (azaz a nagyobb tömegû csillag) kisebb luminozitású, mint egy hozzá hasonló tömegû fôsorozati objektum.
- A fénygörbe a fedésen kívüli szakaszon is erôteljes változást mutat. A fedési és fedésen kívüli szakaszok nem különíthetôk el. A másodminimum mélysége több, mint 70%-a a fôminimum mélységének. Ez arra utal, hogy a komponensek felületi fényessége közel megegyezik. Ez azt az elôzôekben feltett állítást is megmagyarázza, hogy a színindex nem, vagy nagyon kicsit változik.
- A fénygörbék és radiális sebesség görbék egyidejû tanulmányozásából két al-csoport különíthetô el (Binnendijk, 1970): A-típus: a fôminimum tranzit; W-típus: a fôminimum okkultáció. Az utóbbi rendszerek fénygörbéi kevésbé stabilak. (Ismeretes, hogy több olyan rendszer van, melyek oszcillálnak a két típus között, pl. TZ Boo, CV Cyg.)
- A spektrumvonalak erôs kiszélesedést mutatnak, bizonyos fázisokban kettôzôdés is elôfordul. Az ultraibolya tartományban mért kromoszférikus emisszió intenzitása alapján a W UMa rendszerek a legaktívabb késôi típusú csillagok közé tartoznak (Dupree, 1983).
- Az UBV- és uvby-fotometriai mérések alapján a keringési periódus és színindex között korreláció mutatkozik: a hosszabb periódusú kettôsök kékebbek (periódus-szín reláció).
Nem konvektív, fôsorozati csillagokból álló kontakt rendszerek esetén fontos megemlíteni, hogy q nem= 1 esetén nem alkothatnak kontakt rendszert (Kuiper, 1941). Ez a fôsorozati csillagok tömeg-sugár, és a Roche-geometria elméleti tömeg-sugár összefüggése közötti ellentmondás következménye: R2/R1=qa, ahol a kb= 0,46 érintkezô rendszerekre, fôsorozati (egyedi) csillagokra azonban a > 0,6. Kuiper „jóslata" azonban ellentétben áll a megfigyelésekkel, ugyanis a legtöbb kontakt rendszerre q kb= 0,3, míg q= 1 tömegarányú W UMa típusú csillagot még nem találtak. E paradoxon feloldását jelenti, hogy a kontakt kettôs rendszert egy konvektív burok veszi körül, ami a belsô Lagrange-felületen túlnô (Lucy, 1968). Ebben az esetben nem érvényes a fenti tömeg-sugár összefüggés. A nem túl vastag réteg az energiatranszportot teszi lehetôvé a komponensek között. Ez magyarázatot ad a mellékkomponens többletluminozitására és a szinte azonos felszíni hômérsékletre.
Problémák merülnek fel a W UMa-típusú kettôsök keletkezésével kapcsolatban is. Valószínû, hogy a nullkorú, fôsorozathoz közeli csillagok (W-típusú rendszerek) kontakt rendszerként keletkeztek. Az idôsebb, fôsorozati komponensekbôl álló rendszerek (A-típusúak) azonban jelentôs impulzusmomentumot vesztve, pl. mágneses fékezéssel fejlôdtek kontakt objektumokká. Az is elképzelhetô Webbink elmélete szerint, hogy a nagyobb tömegû csillag lassan bekebelezi a mellékkomponensét, s így a W UMa rendszer gyorsan forgó, G- K színképosztályú óriássá alakul (FK Comae csillagok).
Periódusváltozás kettôs rendszerekben
A fedési kettôsök keringési periódusa általában nem állandó, hanem többféle ok miatt változhat. Ezek közül a legfontosabbak a következôek:
Periasztronmozgás (apsidal motion): a pálya nagytengelye elfordul a látóirányhoz képest.
Fény-idô-effektus (light time effect): a Doppler-effektus miatt hosszabb-rövidebb periódust mérünk (idôpontok eltolódnak).
Tömegátadás (mass transfer): a periódus ilyen esetben közel egyenletesen nô vagy csökken.
Ezek közül leggyakrabban a tömegátadás fordul elô. Ez nyilván csak félig érintkezô illetve kontakt rendszerek esetén következhet be.
A periódusváltozás ütemére egyszerû becslés adható akkor, ha feltesszük, hogy a tömegátadás során a rendszer össztömege állandó marad. Ekkor a rendszer teljes (állandó) impulzusmomentuma:
J = (G A / M)1/2 (m1 m2) .
Tegyük fel, hogy m1 ad át Dm tömeget m2-nek. Ekkor Kepler III. törvényét felhasználva adódik:
(1/P) DP/Dt = 3 (m2–m1) / ( m1 m2) Dm/Dt.
Evolúciós szempontból 3 tömegátadási típust különböztetnek meg:
A-típus: a tömegátadás a magbeli H-égéskor következik be.
B-típus: a tömegátadás a He-héj égetése elôtt következik be.
C-típus: az átadás a He-héj égetésekor, a szén-égés elôtt indul meg.
Dinamikai szempontból a tömegcsere lefolyása lehet „gyors", ekkor a nagyobb tömegû csillag ad át tömeget a kisebb tömegû társának, és a kitöltöttség fokozódik. Illetve lehet „lassú", ekkor a nagyobb tömegû csillag Roche-térfogata nô.
Mûszertechnikai áttekintés
A Bajai Bemutató Csillagvizsgáló 1955. december 18-án nyílt meg a belváros-ban, a felsôlégkör kutatása céljával. 1987-ben az MTA átadta a Bajai Bemutató Csillagvizsgáló intézetet a városnak, így a kutatás és ismeretterjesztés kettévált: a kutatóintézet kiköltözött a centrumtól kb. 6 km-re (keletre). A kutatómunka fokozatosan a szoros kettôscsillag rendszerek asztrofizikája irányába tolódott el. Az akkori 40 cm-es Cassegrain távcsô a JATE tulajdona volt, ezért Szegedre került, majd késôbb Baja városa megkapta a támogatást egy új távcsô beszerzésére. A jelenlegi teleszkópról az alábbiakban szólok.
A távcsô: Méréseimet az 50 cm tükörátmérôjû, f/8-as fényerejû, 4,2 m fókusztávolságú, villás szerelésû, Ritchey-Chrétien teleszkóppal végeztem Baján, 2000. június 26-30. között.
Az optikai elrendezés: A viszonylag rövid fókusztávolságú fôtükör egy domború segédtükörre vetíti a fényt, ahol a sugárkúp nyílásszöge csökken, így a második reflexió után egy látszólag a fôtükörnél sokkal kisebb nyílásviszonyú objektív fénymenete halad át a fôtükör furatán. Rövid tubushosszban – a fókusznyújtásnak köszönhetôen - hosszú fókusztávolság rejlik, így a távcsô mechanikailag stabil. A kör alakú leképezés miatt a távcsô CCD használatára nagyon kedvezô.
A CCD detektor: APOGEE AP7 típusú CCD, melynek néhány fontos paraméterét a következô táblázat mutatja:
|
Pixelszám |
512* 512 |
|
Pixelméret |
24*24 mm |
|
A/D konverzió |
16 bit (65535 ADU) |
|
Chip |
SITE, hátsó megvilágítású |
Az utolsó éjszakán (29-én) méréseimet ST-9E típusú kamerával készítettem, melynek a fontosabb paraméterei:
|
Pixelszám |
512*512 |
|
Pixelméret |
20*20 mm |
|
A/D konverzió |
16 bit (65535 ADU) |
|
Chip |
KAF-0261E |
Az optikai CCD detektorok olyan eszközök, melyek apró, mm nagyságrendbe tartozó, mátrixos elrendezésû cellái (pixelei) a fényre érzékenyek, mégpedig oly módon, hogy minden egyes cella a ráesô fénymennyiséggel arányos meny-nyiségû elektront halmoz fel – fotoeffektus útján. A megvilágítás után egy kiolvasó rendszer segítségével a kimenethez „visszük", és itt mérjük meg az egyes pontokhoz tartozó töltésmennyiséget. Így ábrázolható az egyes pixelekhez tartozó, töltéssel arányos fényesség - azaz maga a kép.
A CCD kamerák fôbb jellemzôi:
- Nagy kvantumhatásfok (hátsó megvilágítású CCD esetén elérheti a 80-90%-ot is).
- A vörös és infravörös tartományban jóval érzékenyebb, mint a kékben.
- A töltésmennyiség a beesô intenzitásnak több nagyságrenden keresztül lineáris függvénye (nagy a dinamikai tartománya).
- Térbeli felbontása roszabb, mint a fotolemezé, de CCD–vel rövidebb idô alatt halványabb objektumokat jeleníthetünk meg.
- Mint mindegyik mérôeszköz, a CCD is rendelkezhet véletlenszerû és szisztematikus hibával. Fontos megemlíteni a sötétzaj (elektronok foton nélkül is lesznek), illetve a kiolvasási zaj szerepét (bôvebben l. Fûrész, 1998).
A CCD felvételeket jellemzô tényezôk kiszûrése és explicit figyelembe vétele nem elhanyagolható. Ezen kalibrálások a következôképpen alkalmazhatóak:
Sötétzaj korrekció: a sötétzaj korrelált – bizonyos pixelek mindig több elektront vesznek magukba – ami ún. sötétkép késyítésével vehetünk figyelembe. A sötétképet digitálisan levonjuk az elkészített képbôl:
I’ (x,y) = I (x,y) – D (x,y) .
Az eredménynek is lesz hibája, hogy ezt csökkentsük, átlagolnunk kell a sötétképeket:
D = 1/N* S Di (x,y).
Bias korrekció: azt mondja meg, hogy 0 expozíciós idônél adott pixelhez hány elektron tartozik. Szintén átlagolni kell; elônyös, hogy gyárilag beépítik a bias–kép készítést a kamerákba. A sötétzaj-korrekcióval egyben a bias-korrekciót is elvégezhetjük.
Overscan korrekció: Az overscan egy elzárt terület a CCD-n, ahol a bias szint ingadozását figyelhetjük meg. Ennek elônye: nem kell külön bias képet készíteni. Csak utólag nézik az intenzitást, függvényt illesztenek rá, az értékét a képbôl levonják.
Flatfield korrekció: Az egyes pixelek eltérô érzékenységét veszi figyelembe. Azonos fényességhez nem ugyanolyan intenzitás tartozik, melynek okai lehetnek pl. porszemek (diffrakciós gyûrûk) illetve a beállítási hibák. Elôször az egyenletesen megvilágított látómezôrôl ún. flatfield képeket készítünk, átlagoljuk ôket, majd korrigáljuk a bias-szintre és egyre normáljuk. Végül ezzel leosztva a korrigálni kívánt képet, visszaállíthatjuk a helyes intenzitás-eloszlást.
A csillagok kiválasztása
Az FU Dra csillagot a http://astro.estec.esa.nl/Hipparcos/HIPcatalogueSearch.html címen elérhetô Hipparcos adatbázisból választottam ki. A kiválasztás legfontosabb szempontjai az alábbiak voltak:
- Olyan csillagot kell találni, mely a megfigyelések alatt lehetôleg egész éjszakán át mérhetô.
- A fényessége ideális legyen - CCD detektor használata esetén ez az érték kb. 9-13 magnitúdó közé essék.
- A periódusa ne legyen 1 ill. 0,5 nap, mert ekkor ugyanabban a fázisban tudnánk észlelni; valamint, kevés észlelési idô esetén a rövid, 1 napnál kisebb periódusú csillagok jöhetnek számításba.
- A mérés idejét nem célszerû úgy választani, hogy az éppen telihold környékére essék.
Az objektum kiválasztásakor megkerestem a számomra legfontosabb paramé-tereket, melyeket az 1. táblázat sorol fel.
|
RA |
15h34m45s |
|
DEC |
+62º16'44,9" |
|
Minimum fényesség (V) |
11,098 magnitúdó |
|
Maximum fényesség (V) |
10,551 magnitúdó |
|
Periódus |
0,3067180 nap |
1. táblázat: Az FU Dra megfigyeléséhez szükséges paraméterek
Az FU Dra egy W UMa típusú változó, melynek minimum és maximum fényessége V-szûrôvel 10,551 és 11,098 magnitúdó, ami a detektálás szempontjából nagyon kedvezô. A fényváltozás periódusa 0,3 nap körüli, ami 7,2 órának felel meg. Egy nyári éjszaka során - kedvezô légköri viszonyok mellett - fél periódus kimérésére van lehetôség, s a következô éjszaka során más fázisban figyelhetô meg a csillag. Az objektum kiválasztásánál nem elhanyagolható szempont volt, hogy a szakirodalom viszonylag kevés mérési eredményt közölt errôl a csillagról. Az FU Draconis-ról mérési adatot nem közöltek még, így mindössze a Hipparcos adatbázisban közölt periódus és fénygörbe volt ismert. Mérésem célja így elsôsorban az volt, hogy új minimum idôpontokat határozzak meg, és a periódus értékét pontosítsam. A Guide 7.0 program segítségével készítettem keresôtérképet; mivel az adott távcsô és CCD kamerák esetén (l. fentebb) a látómezô 9x9, illetve 10x10 ívperc, így a keresôtérkép készítésekor ekkora látómezôben gondolkodva összehasonlító csillagokat is kellett találni a csillag fényességváltozásának hitelesítésére. A Guide segítségével meggyôzôdtem arról, hogy a kiválasztott összehasonlítók esetében eddig nem tapasztaltak fényességváltozást.
Az FU Dra mellett a másik kiválasztott objektum az AW UMa volt, amely régóta ismert fedési változó. A kiválasztásban az alábbiak játszottak döntô szerepet:
- A csillagról sok elérhetô publikáció illetve mérés legyen (fénygörbe és radiális sebesség adatok)
- W UMa típusú fedési kettôs
- Rövid periódus
- Viszonylag fényes objektum
Az AW UMa megfigyelési paraméterei a 2. táblázatban találhatóak.
|
Min. fényesség (V) |
7,13 mag |
|
Max. fényesség (V) |
6,83 mag |
|
Epocha (JD) |
44664,7993 |
|
Periódus (nap) |
0,4387299 |
2. táblázat: Az AW UMa kiválasztásához szükséges fontos paraméterek
AZ AW Ursae Majoris és az FU Draconis fizikai paramétereinek meghatározása
AW UMA
I. Irodalmi feldolgozás
Az AW UMa régóta ismert W UMa típusú kettôscsillag. A Roche-geometriával jellemezve kontakt rendszer, tehát a komponensek érintik egymást. A fénygörbe illetve a fázisdiagram tanulmányozása révén a mellékminimumnál totális fedés figyelhetô meg, ami arra utal, hogy a fôkomponens felületi fényessége a nagyobb, valamint a pályasíknak a látóiránnyal bezárt szöge (inklináció) 90º-hoz közeli, azaz A-típusú kontakt rendszer (Binnendijk, 1970). A jelenlegi ismeretek alapján ez a legkisebb tömegarányú rendszer (0,07<q<0,08). A radiális sebességgörbébôl számolt tömegarány az eddigi mérések és számítások alapján jó egyezést mutat a 3. táblázatban felsorolt értékekkel (McLean, 1981):
|
Tömegarány |
Hiba |
Publikáció |
|
0,079 |
0,008 |
Mochnacki & Doughty, 1972 |
|
0,0716 |
0,0005 |
Wilson & Devinney, 1973 |
|
0,0795 |
0,0005 |
Lucy, 1973 |
|
0,0766 |
0,0008 |
Nagy, 1974 |
3. táblázat: Az AW UMa rendszer lehetséges spektroszkópiai tömegarányai
A spektroszkópiai elemzések révén korai spektráltípusú: F1-F2 (Eggen, 1967), vagy F0-F1 (Paczynski, 1964). A rendszer periódusváltozását régebben értelmezték úgy is, hogy konstans szakasz után hirtelen (ugrásszerû) perióduscsök-kenés következett be (Hrivnak, 1982), azonban nem vetették el a periódus folyamatosan csökkenését sem. A kettôscsillag össztömege q= 0,0716 tömeg-arány és i= 79°-os inklináció esetén M= 3,5 M¤ . A nagyobb csillag ad át tömeget a kisebbnek, a periódus folyamatos változása és a perióduscsökkenés ezzel megmagyarázható (Hrivnak, 1982).A komponensek nagy felületen érintkeznek, a térbeli mozgásból arra következtetett Derman, Demircan és Müyesseroglu (1990), hogy ún. öreg korong-populációs csillag. Hrivnak (1982) számításai alapján mindmáig alkalmazott legfontosabb paramétereket a 4. táblázat mutatja:
|
Periódusvált. üteme |
-3,2*10-10 nap/ciklus |
|
Tömegátadás üteme |
5,1*10-10 M¤ /év |
|
Teff(1) |
7175 K |
|
Teff(2) |
6910 K vagy 7146 K |
|
i |
79,1º |
4. táblázat: Az AW UMa paraméterei Hrivnak (1982) számításai alapján
II. A periódusváltozás vizsgálata
A W UMa típusú fedési változóknál a periódus idôben változik, aminek lehetsé-ges oka az ezen rendszerekben elôforduló tömegátadás. Ahhoz, hogy a változás mértékérôl, típusáról mondjunk valamit, O-C diagramot kell készítenünk. Ez a diagram idôtartamokat ábrázol. Fedési változók esetén az O, obszervált idôpontot a fôminimum adja, C pedig a minimum bekövetkezésének várható idôpontja (kalkulált). Legyen T0 a referenciaidôpont (epocha), N pedig a referenciaidôponttól eltelt ciklusok száma. Válasszunk ki egy számunkra megfelelônek látszó próbaperiódust (P). Ekkor a fôminimum várható bekövetkezését a TN= T0+NP összefüggésbôl számíthatjuk ki. Így megkaphatjuk az O-C érté-két O-C= T*–(T0+NP), ahol T* egy megfigyelt fôminimum idôpontja.
A görbe alakja meghatározza a periódust oly módon, hogy ha:
- ferde egyenes, akkor a periódust rosszul becsültük meg: O-C=N(P*-P)=NA, ahol A az egyenes meredeksége. Ha az A pozitív, akkor P* nem változik, P-t alulbecsültük. Ekkor új P’-t definiálva P’=P+A, illetve ha A negatív volt,
P’=P-A. Ez esetben a periódus korrigálásra szorult.
- a periódus ciklusról ciklusra egyenletesen változik, akkor
O-C= (T*-T0)+N{( P*0-P)-D P/2}+)-D PN2/2 (1)
ahol P a próbaperiódus, T0 az alapidôpont, a P*0 pedig a T0-hoz tartozó valódi periódus. Ez egy parabola alakú függvényt eredményez, melynek általános alakja An2+Bn+C. Innen A=D P/2, tehát a periódusváltozás ütemé-neka felét adja. (Az O- C deriváltjának segítségével megadható a periódus-korrekció.) A
P*N=P*0+ND P (2)már említett összefüggésbôl tehát megkapjuk, hogy most mennyi a csillag periódusa.
50 évre visszamenôleg összegyûjtöttem, majd feldolgoztam a periódusváltozására vonatkozó adatokat, valamint megszerkesztettem a rendszer O-C diagramját, amelyet az 1. ábra mutat.
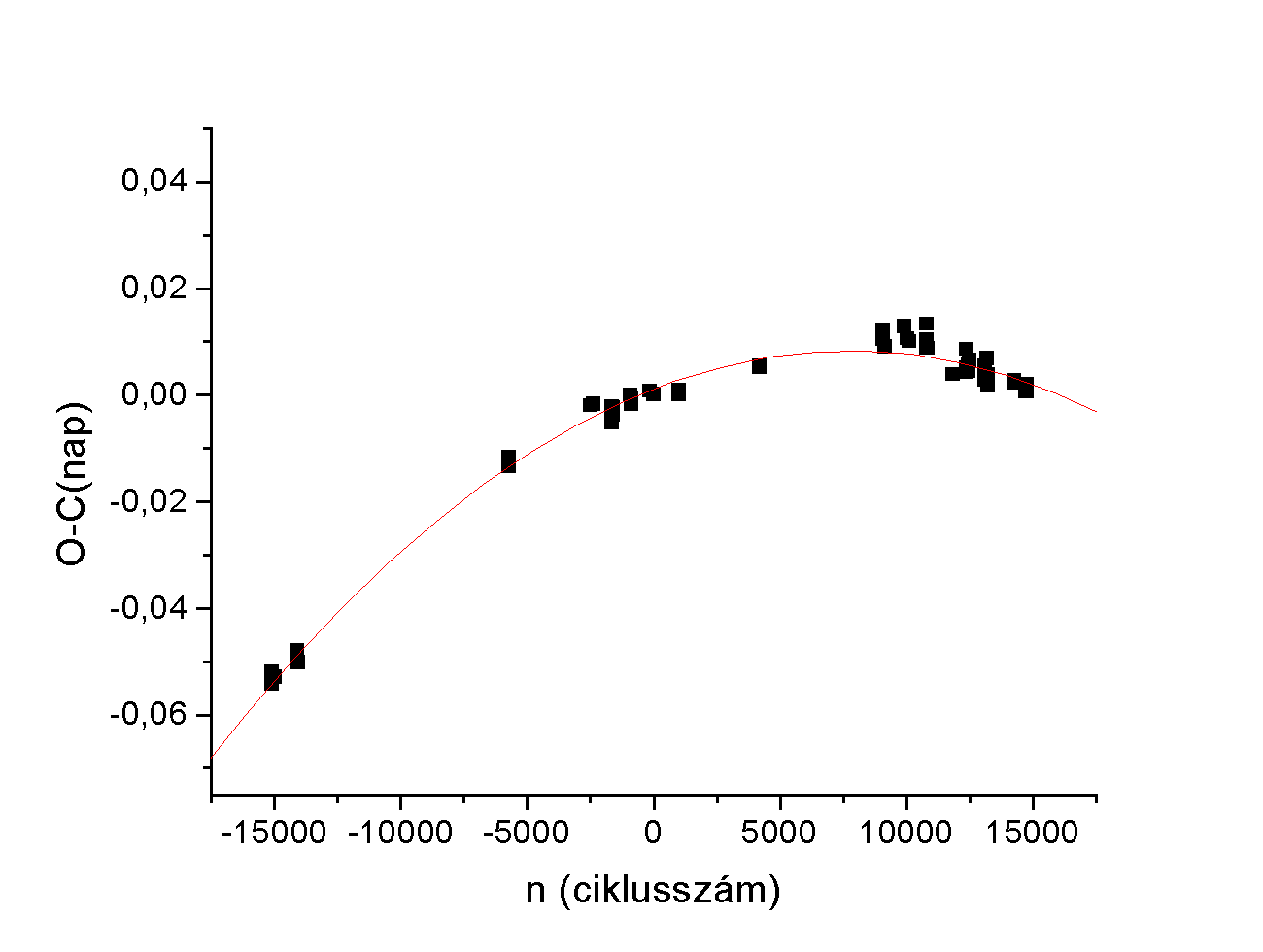
1.ábra: Az AW UMa O–C diagramja
A lefelé tartó parabola arra utal, hogy a rendszer periódusa ez idô alatt folyamatosan csökkent, és a periódus idôben ténylegesen változik. Az illesztett függvény paraméterei a következôk:
A = –1,193525*10-10
B = 1,849505*10-6
C = 1,175979*10-3
Ezen paraméterek,az irodalomból összegyûjtött adatok, valamint a fentiekben említett (2) összefüggés alapján a rendszer orbitális periódusa: P= 0,4387279 nap, melynek t0= 2444664,7993 JD az epochája.
A periódusváltozás üteme (1) alapján DP= 2,38704*10-10 nap/ciklus.
III. Fizikai paraméterek meghatározása
A komponensek radiális sebességeit McLean (1980) adatai alapján ábrázoltam, majd görbeillesztéssel spektroszkópiai tömegarányt határoztam meg. Az AW UMa sebbességgörbéjét a 2. ábra mutatja.
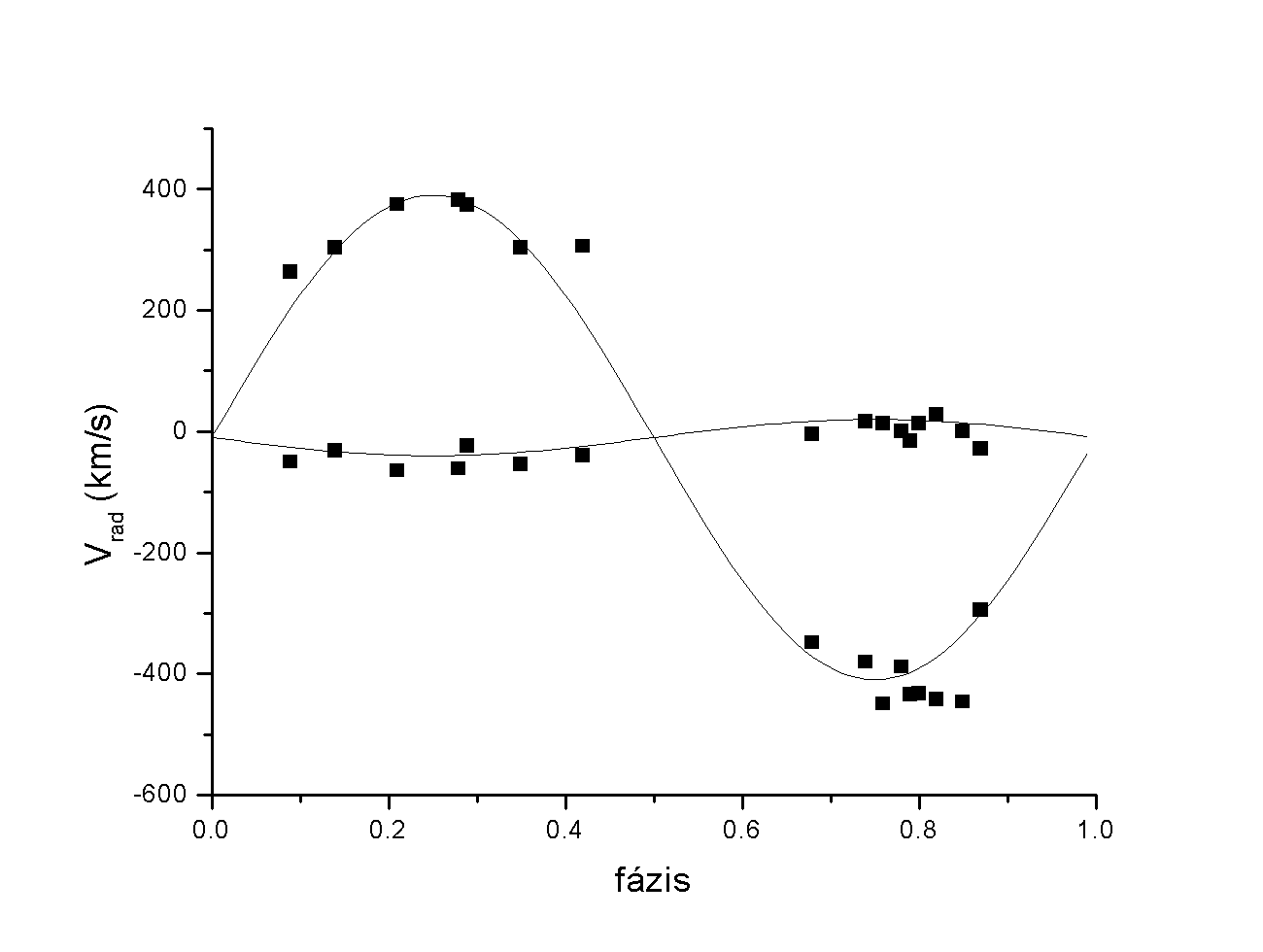
2. ábra: Radiális sebességgörbe az AW UMa rendszerrôl.
A fenti radiális sebesség görbére K sin(2p f) + v0 alakú függvényeket illesztettem, ami azt az egyszerûsítô feltevést jelenti, hogy a mért radiális sebességek a csillagok tömegközéppontjának keringését írják le. Az illesztés segítségével a sebesség-amlitúdókra K1= 30 km/s (fôkomponens) és K2= 400 km/s (mellék-komponens) értékeket kaptam eredményül. A fedési kettôsök tömegarányát az amplitudók aránya határozza meg. Az általam számolt érték q= 0,075.
A csillag spektráltípusa F0-F1 - legalábbis a publikációkban ez a leggyakrabban elfogadott - ehhez 7000 K-hez közeli hômérséklet tartozik.
Az spektroszkópiai elemzésbôl kapott tömegarányt a késôbbiekben a Fénygörbe modellezés fejezet Tesztelés alfejezetében a fénygörbeillesztésnél is fel-használom.
A Hrivnak (1982) publikációjában közölt össztömeget (M= 3,5 M¤ ), valamint az elôzôekben meghatározott tömegarányt (q= 0,075) alapul véve kiszámítottam a komponensek tömegét:
m1= 3,2558 M¤ és m2= 0,2442 M¤ .
A Schmidt-Kaler-féle táblázatokat használva (Carroll & Ostlie, 1996) a tömegüknek megfelelô színképtípusuk B9 illetve M5. A ténylegesen megfigyelt színképtípus mindkét csillagra F0-F1, ami arra utal, hogy a kontaktus miatt a komponensek felszíni hômérséklete kiegyenlítôdik.
Kepler III. törvénye segítségével kiszámítottam a kettôs rendszer keringési pályájának fél nagytengelyét az elôzôekben közölt periódusértékkel:
A = (G*M*P2/4p2)1/3
A pálya fél nagytengelyének nagysága közelítôen: A = 3,694 ± 0,047 R¤
(mely érintkezô rendszerek esetén kb. a komponensek sugarainak összege). A Roche-geometriából adódóan az alábbi közelítô képleteket alkalmazva meghatároztam a komponensek sugarát:
R1 = A*{0,38–0,2*log(q)} R1 = 2,24 R¤
R2 = A*{0,38–0,2*log(1/q)} R2 = 0,57 R¤
A sugarak alapján A2 és M2 a komponensek színképtípusa. Az eredményen látható, hogy a kapott R2 érték nagyobb, mint ami a csillag tömege alapján indokolt lenne.
A perióduscsökkenés mértékébôl meg lehet határozni a tömegátadás mértékét a kettôscsillagra, ha ismerjük a komponensek tömegét:
d ln(P) / dt = 3 (m2 - m1) /(m1 m2) (dm / dt),
ahol dm a dt idô alatt az m1 tömegû csillagról az m2-re átáramlott tömeget jelenti. Az általam meghatározott O-C diagram alapján évente kb. 5*10-8 naptömegnyi anyag áramlott át a nagyobb tömegû csillagról a kisebbre. Ez jó egyezést mutat Hrivnak (1982) eredményével. Ez a tömegátadási ráta árulkodik arról is, hogy melyik komponens biztosítja az anyagátáramlást. Ha negatív az értéke, akkor a nagyobb tömegû összetevô veszít tömegébôl, csökkentve ezzel a rendszer keringési periódusát.
FU Dra
I. Képeim feldolgozása, kiértékelése
A CCD-vel készült digitális felvételeimet az IRAF csillagászati képfeldolgozó rendszer segítségével mértem ki. A CCD képek elkészítésével egyidôben készítettem a sötétképeket, amiket a mérés során használt kameravezérlô program automatikusan le is vont a képekbôl, így a dark korrekciót utólag már nem kellett elvégeznem. A képek 10-es sorozatokban készültek, minden egyes sorozat elején egy-egy újabb sötétkép készült, s ezt a képet vonta le a program minden képbôl. A flat korrekció elvégzéséhez mind az esti, mind a hajnali szürkületben készítettem több flatfield képet is, különbözô átlagintenzitásúakat (10 és 45 ezer ADU közötti átlagok), s ezekbôl utólag az IRAF flatcombine taszkjának segítségével, medián átlagolással készítettem minden egyes éjszakára egy-egy flatfield képet. A csillagok fényességmérését szintén az IRAF-ben végeztem, egyszerû apertúra fotometriát használva (aphot). Az apertúra sugarait az egyes képeken az imexam taszkkal vizsgálva határoztam meg, figyelembe véve a csillagprofilok félértékszélességét. Az aphot taszkot interaktív módban futattam, ezáltal biztosítva, hogy a kimenô adatfile elsô oszlopában mindig a változó, második és harmadik oszlopában az összehasonlító és az ellenôrzô csillagok fényességértékei szerepeltek. Mivel szûrôt technikai opkokból nem használtam, ezért nem végeztem semmilyen korrekciót a kapott eredményeken (standard transzformáció), a késôbbiekben az instrumentális magnitúdókat használtam fel. Az alkalmazott differenciális fotometria során a CCD kis látómezeje miatt az extinkciós korrekciót sem kellett
végrehajtani. A fényességmérés pontosságát mutatja az összehasonlító (c1) és az ellenôrzô (c2) csillagok fényességének különbsége, mely a 3. ábrán látható:
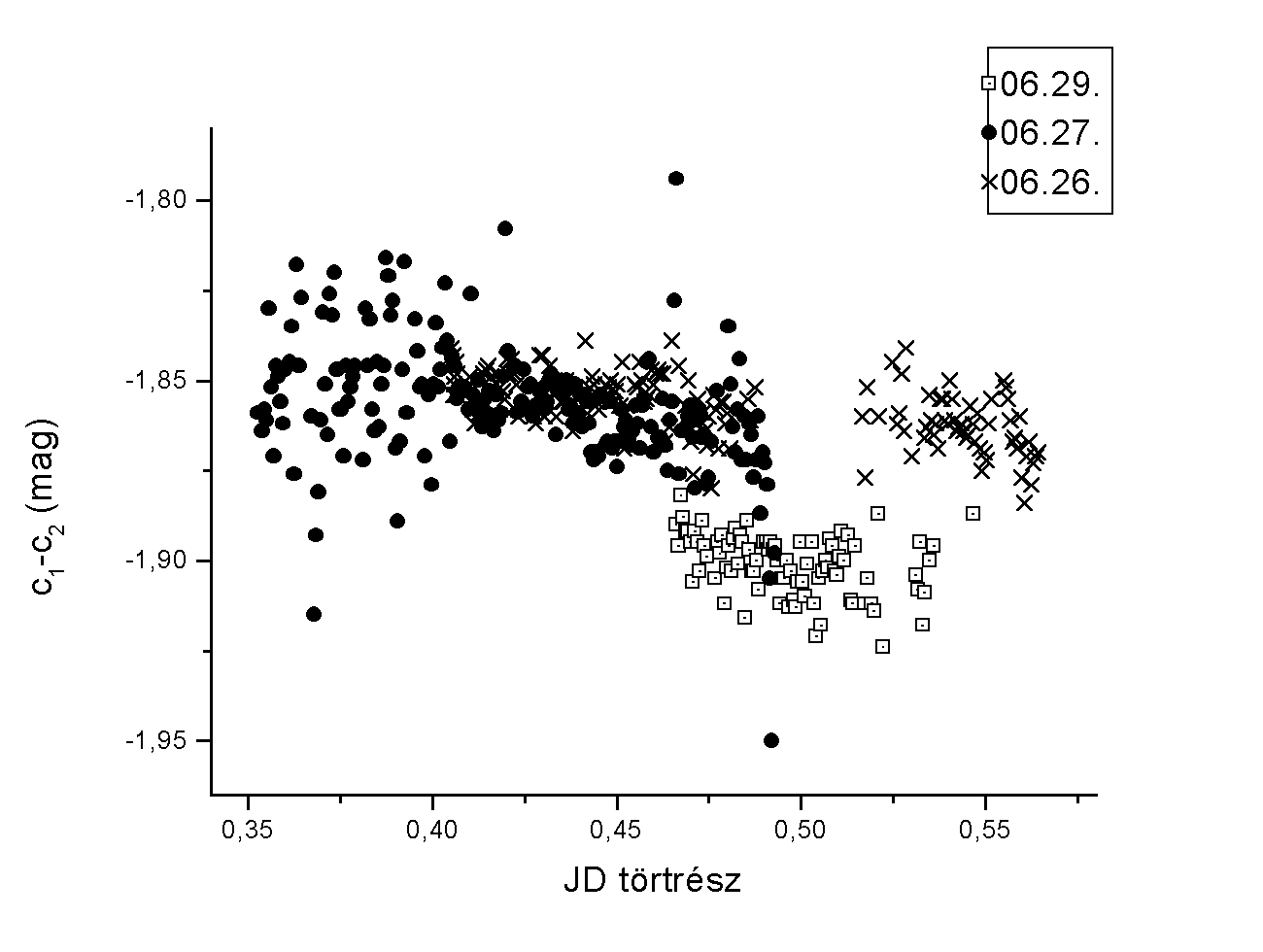
3.ábra: Az FU Dra rendszer mérése során az összehasonlító és az ellenôrzô csillagok különbsége
A grafikonról leolvasható, hogy az égbolt minôsége erôsen változott, nem csak napról napra, hanem egy éjszakán belül is (a szórás néhol 0,01, másutt 0,04 magnitúdó), ezt egyébként a mérés során megfigyelt átmeneti felhôsödés magyarázza. A 29-én készített képeken hirtelen ugrás figyelhetô meg, ami egyrészt a nem túl tiszta égbolttal, másrészt más kamerával (ST-9E) készített képekkel magyarázható.
A fénygörbe elkészítéséhez szükség volt az egyes felvételek elkészítésének idôpontjaira, amit a FITS képek fejléceibôl szedtem ki. Az óra-perc-másodperc formátumú fájlba írt adatokat egy program segítségével számítottam át JD-re. A fázisdiagram elkészítéséhez szükség volt a periódus értékének meghatározásához. Ezt szintén program segítségével végeztem. A program fázisdiszperziós módszert alkalmaz, a próbaperiódusok szélsôértékeit a Hipparcos katalógus alapján adtam meg. A mérési adatokat fázisba rendezve a 4. ábrán látható görbét kaptam.
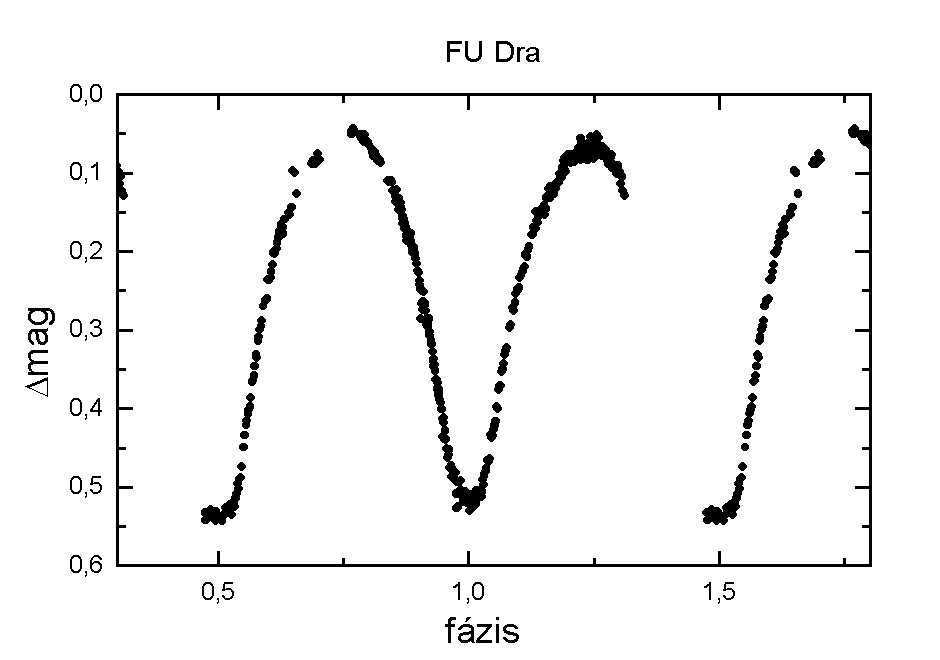
4.ábra: Az FU Dra fázisdiagramja
A fázis definíciója: f= int((t-t0)/P) , ahol t0 : epocha, t: idôpont (JD), P: periódus
II. Perióduskorrekció
A fénygörbe alapján új minimumidôpontokat határoztam meg (a heliocentrikus korrekciót is figyelembe véve):
Tmin II = 2451722.4762 HJD
Tmin II = 2451723.3979 HJD
Ezekbôl a minimumidôpontokból és a Hipparcos epochájából megszerkesztettem a rendszer O-C diagramját, mely az 5. ábrán látható.
A pontokra illesztett egyenes meredeksége:
A = –1,12027*10-6 ± 1*10-7 nap / ciklus
A korrigált periódus: Pcor = Po-c+DP , ahol DP= A * 1 ciklus
Pcor = 0,3067169 ± 1*10-7 nap
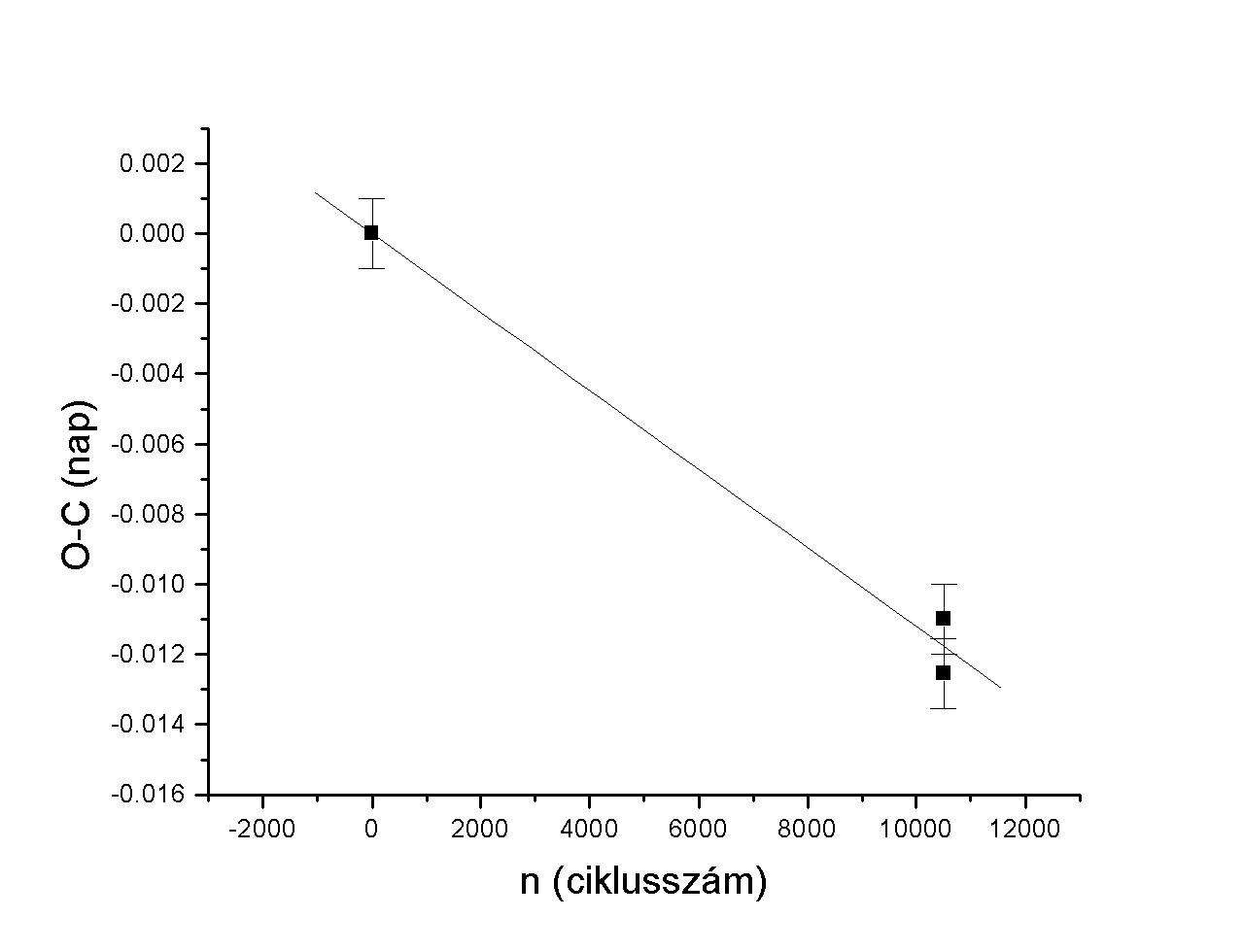
5.ábra: A FU Dra O–C diagramja
Látható, hogy a Hipparcos által megadott periódust kismértékben, de szignifikánsan korrigálni kellett ahhoz, hogy a helyes periódust megkapjuk. A 10-7 nap pontosság eléréséhez több, mint 10000 ciklusnak (azaz kb. 8 évnek) kellett eltelnie.
III. Radiális sebességek
A FU Dra radiális sebességeit Rucinski, Lu & Mochnacki (2000) publikációjából gyûjtöttem össze. Ezekbôl megszerkesztettem a kettôscsillag radiális sebességgörbéjét, majd illesztés segítségével kiszámítottam a rendszer (spektroszkópiai) tömegarányát. A radiális sebességeket a 6.ábra mutatja:
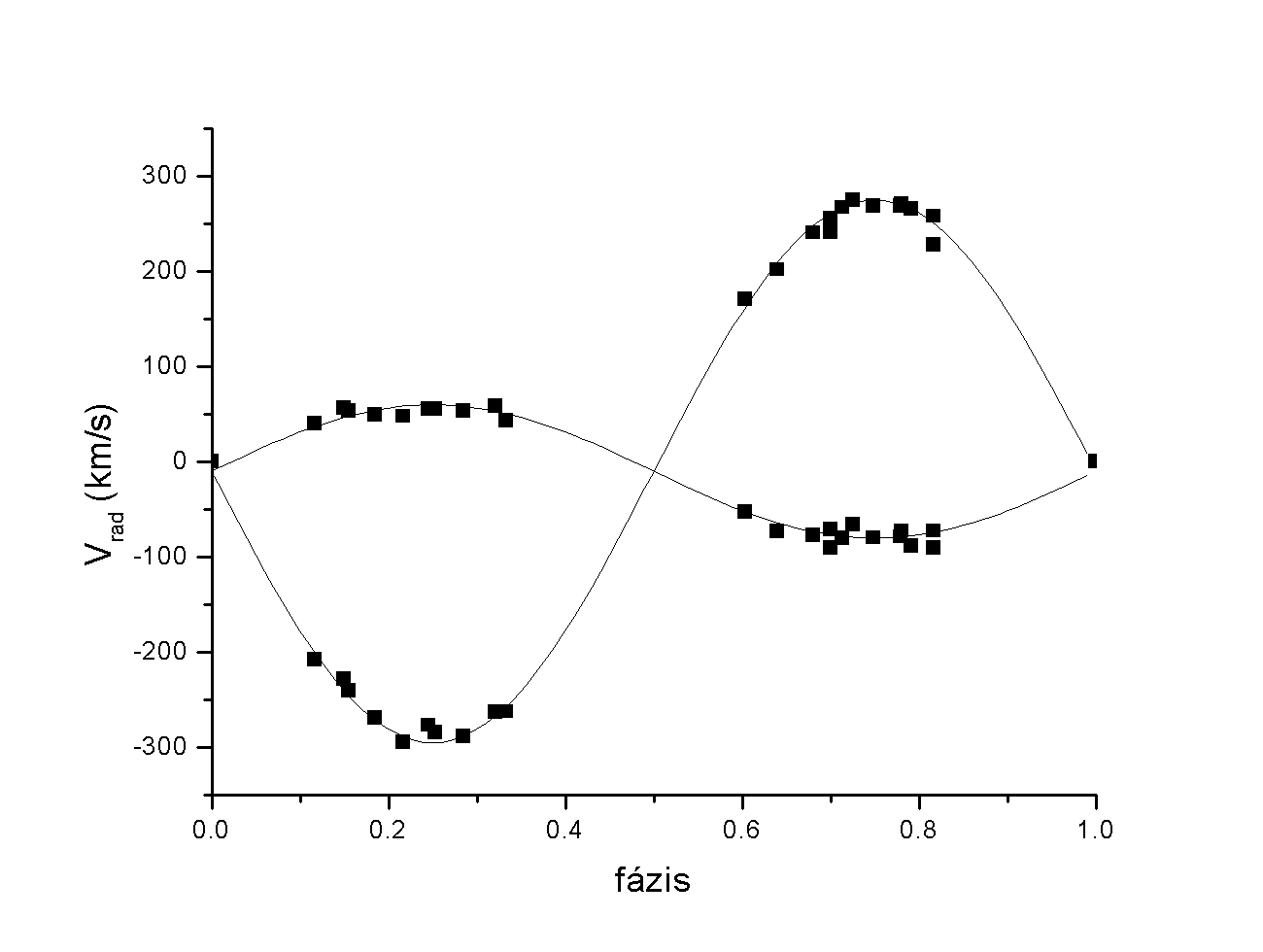
6.ábra: A FU Dra radiális sebesség görbéje
A görbe sebesség-amplitúdóira K1= 70 illetve K2= 285 km/s értékeket kaptam.
Ebbôl a tömegarány q= 0,25.
Ahhoz, hogy a komponensek tömegeit meghatározhassam, az inklináció ismeretére van szükség. A pálya hajlásszögét a fénygörbébôl lehet meghatározni. A továbbiakban ezért a FU Dra fénygörbéjének analízisével foglalkozom.
Fénygörbe modellezés
A NIGHTFALL program
Az Internetrôl publikusan elérhetô www.lsw.uni-heidelberg.de/~rwichman/Nightfall.html program megadott paraméterek alapján modellezi a kettôs rendszert. A modell a Roche-geometrián alapul, figyelembe véve a szélsötétedés és a reflexió hatásait is. Lehetôséget biztosít megfigyelési adatokra történô paraméter-illesztésre is.
A rendszer modellezéséhez az alábbi paraméterek szükségesek:
- periódus
- össztömeg
- félnagytengely (kontakt rendszernél a komponensek sugarainak összege)
- inklináció
- tömegarány
- a Roche-térfogat kitöltöttsége mindkét komponensre
- a komponensek effektív hômérséklete
A hômérsékletek, a kitöltési faktor, a tömegarány és az inklináció illeszthetô paraméterek.
A program tesztelése
Az AW UMa régóta figyelemmel kísért fedési kettôs, így számos mérési adata illetve fizikai paramétere ismert. Ezen okból kifolyólag e rendszer modellezésé-vel teszteltem a programot, így ellenôriztem a számítások hitelességét.
Hrivnak (1982) mérései alapján a megadott intenzitásarányokból magnitúdó értékeket számoltam, majd a kapott fénygörbére illesztettem a modellezô program által számolt fénygörbét. Az illesztett paraméterek a pályasík inklinációja (i) és a rendszer tömegaránya (q) voltak.
A kiindulási paramétereket a 5. táblázat foglalja össze. (A kitöltési faktor mindkét komponensre ugyanaz az érték, ez a Roche-geometriából adódik.)
|
q (= m2 / m1) |
0,075 |
illesztett, jelen dolgozat |
|
i |
79,1º |
illesztett, Hrivnak (1982) |
|
F (kitöltési faktor) |
1,050 |
rögzített |
|
Teff (1) |
7100 K |
Hrivnak (1982) |
|
Teff (2) |
6900 K |
Hrivnak (1982) |
|
P |
0,439 nap |
jelen dolgozat |
|
M (= m1 + m2) |
3,5 M¤ |
Hrivnak (1982) |
|
A |
3,687 R¤ |
jelen dolgozat |
5. táblázat: Az AW UMa modellezésekor használt paraméterek
Az illesztés eredményét a 7.ábra mutatja:
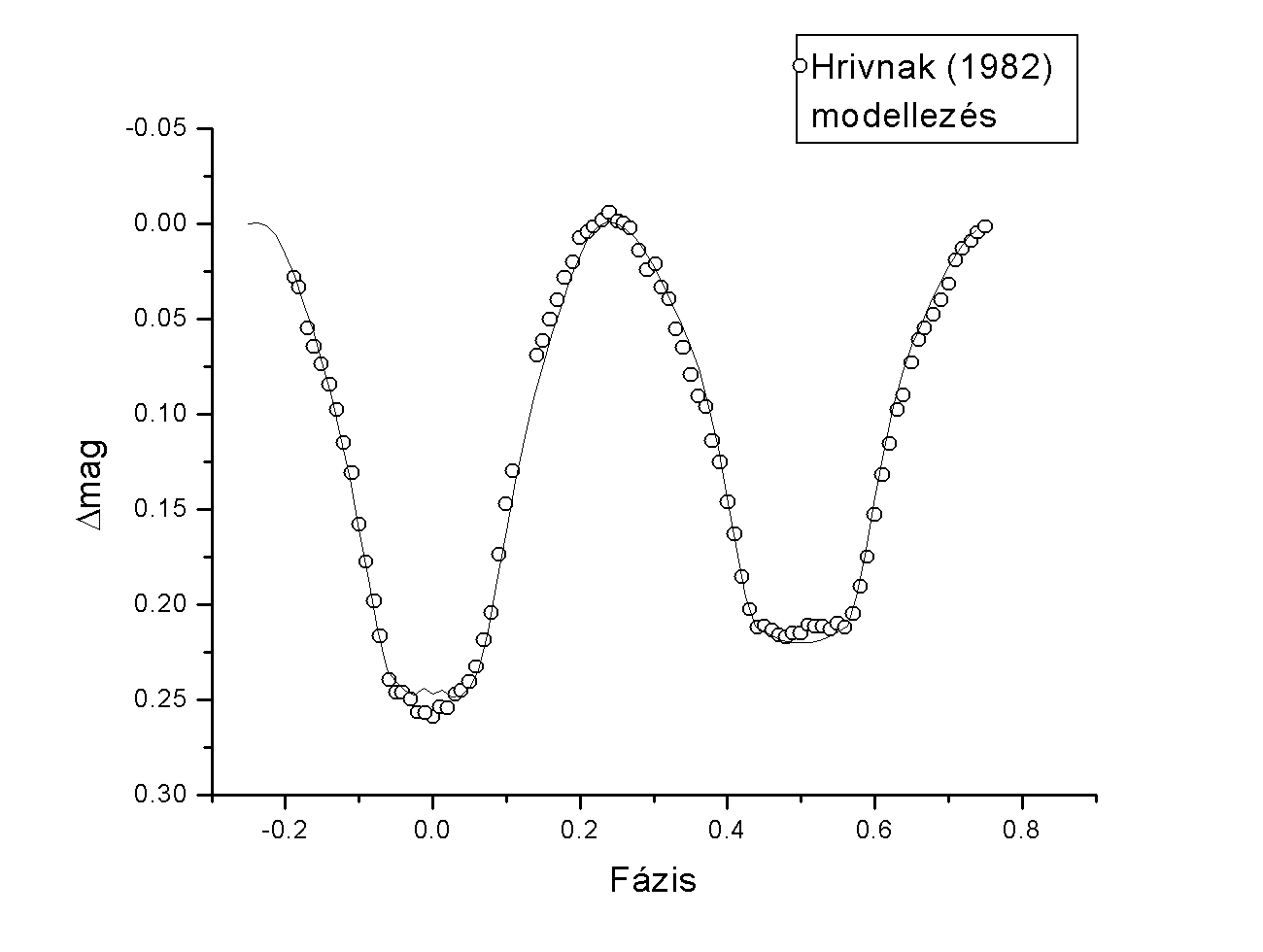
7.ábra: Az AW UMa fénygörbe-modellezés eredményének fázisdiagramja
A fénygörbe-illesztés eredményéül kapott tömegarány és az inklináció:
q = 0,083 és i = 80,66º
Ezek a paraméterek nagyon jó egyezést mutatnak a 3. és 4. táblázatban közölt korábbi irodalmi eredményekkel. A folytonos vonallal ábrázolt modell-fénygörbe láthatóan jól illeszkedik a mérési adatokra (a mellékminimumnál teljes fedést mutat a görbe), így a tesztelés során a program érdemesnek bizonyult a kevésbé ismert FU Dra rendszer modellezésre.
Az FU Dra fénygörbe-modellezése
Az FU Dra általam mért fénygörbéje hiányosságokat mutatott (ismeretlen leszállóág), ezért a teljes fedés kérdéses volt. Így fénygörbe-illesztés segítségével kiegészítettem a méréseimet, és az ismeretlen inklinációt valamint a mellékkomponens effektív hômérsékletét illesztett paraméterként adtam meg.
A tömegarányt és a pálya fél nagytengelyét a radiális sebesség görbe analízisének eredményébôl számítottam ki. A fôkomponens effektív hômérsékletét úgy választottam meg, hogy az megfeleljen a kettôscsillag mért színindexének (B-V= 0.59).
A kapott paramétereket a 6. táblázat foglalja össze.
|
q |
0,25 |
jelen dolgozat |
|
i |
80,8 º |
illesztett |
|
F |
1,05 |
rögzített |
|
Teff (1) |
6200 K |
Hipparcos |
|
Teff (2) |
6505 K |
illesztett |
|
P |
0,307 nap |
jelen dolgozat |
|
M |
1,44 M¤ |
jelen dolgozat |
6. táblázat: Az FU Dra modellezés során használt paraméterei
Az illesztés eredményét a 8. ábra mutatja:
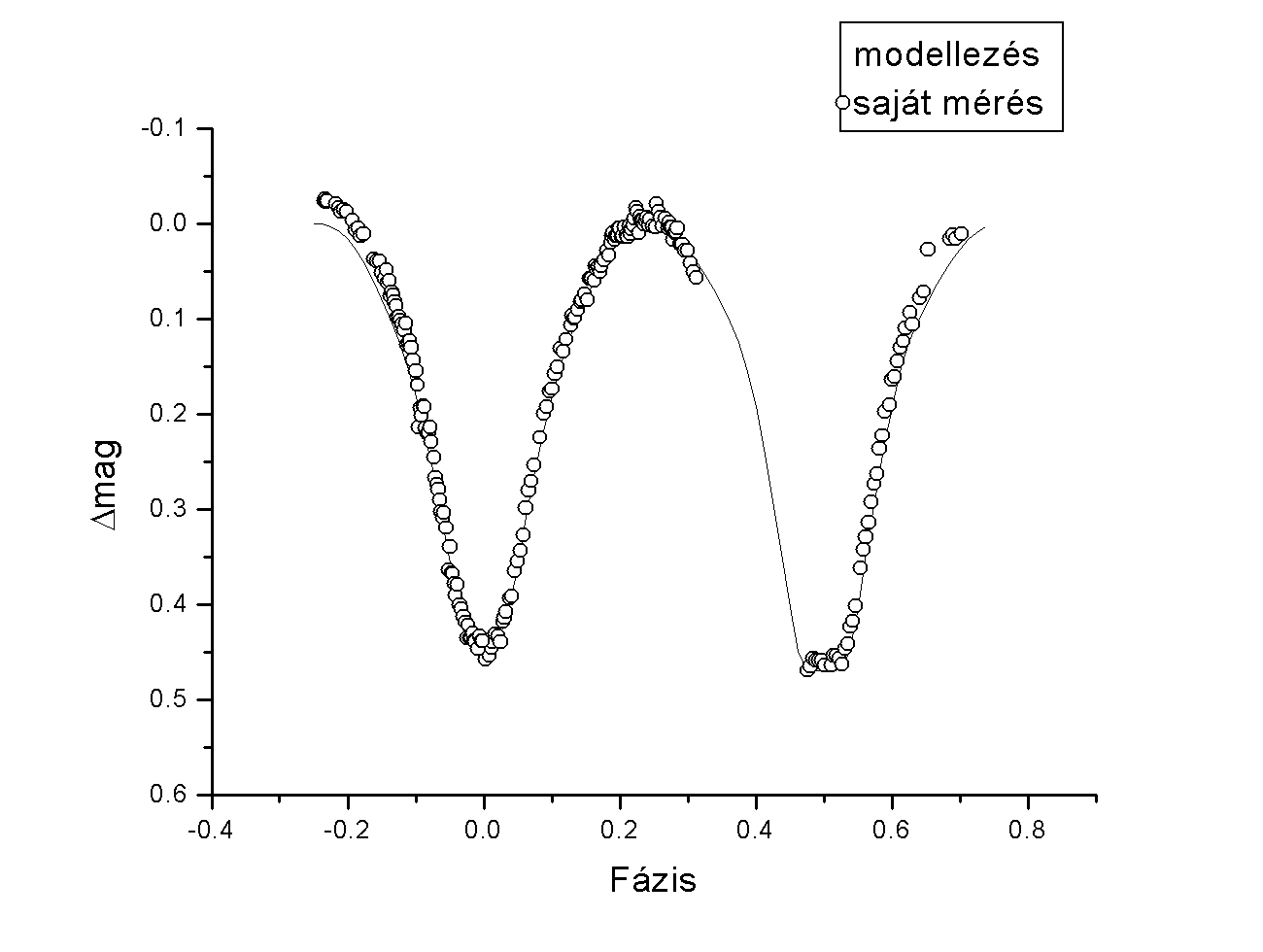
8.ábra: A FU Dra fénygörbe-modellezés eredményének fázisdiagramja
Az illesztés eredményéül az inklinációra, valamint a mellékkomponens effektív hômérsékletére a következô értékeket kaptam:
i= 80,8º
Teff= 6505 K
Mivel méréseim szûrô nélkül készültek, a modellezésbôl kapott hômérséklet nem tekinthetô megbízható becslésnek. A rendelkezésre álló adatok alapján csak annyi állítható, hogy a mellékkomponensnek nagyobb kell, hogy legyen a
hômérséklete ahhoz, hogy a fényváltozást megmagyarázzuk.
Kitûnik a diagramból, hogy a fôminimumnál ténylegesen totális fedés következik be, valamint az, hogy a mellékkomponens effektív hômérséklete a magasabb. Mindez a W-típusú kontakt rendszerek jellemzôje.
A modell-fénygörbe és a mérések magnitúdói jó egyezést mutatnak, ezáltal bizonyítva a rendszer fizikai paramétereinek konzisztens meghatározását.
Az FU Dra fizikai paramétereinek meghatározása
Kepler III. törvényét átírva a számomra megfelelô alakba meghatároztam a kettôscsillag össztömegét:
(K1+K2)3 (P/2p) = sin3(i) G (m1+ m2)
ahol G a gravitációs állandó, K1 és K2 a sebesség amplitúdói, i az inklináció (a fénygörbe-modellezésbôl), M=m1+m2 pedig a komponensek össztömege. Eredményül az alábbi érékeket kaptam:
M = 1,44 M¤
m1 = 0,29 M¤
m2 = 1,15 M¤
Ezek a tömegértékek nagyon hasonlóak a legtöbb W UMa típusú rendszerhez.
Összefoglalás
I. AW UMa érintkezô kettôscsillag
A régóta ismert fedési kettôsnek 50 évre visszamenôleg összegyûjtöttem a minimumidôpontjait, majd meghatároztam az O–C diagramját. Az illesztett parabola segítségével kiszámoltam a keringési periódusát, valamint meg-határoztam a periódusváltozás ütemét. Az eredményül kapott periódus és tömegarány, illetve az irodalomból vett össztömeg segítségével a rendszer fontos fizikai paramétereit meghatároztam. Radiális sebességgörbe-illesztéssel spekt-roszkópiai tömegarányt határoztam meg.
Eredményeimet a 7. táblázat foglalja össze:
|
P (nap) |
0,4387279 |
|
periódusváltozás üteme (nap/ciklus) |
2,38704*10-10 |
|
m1 (M¤ ) |
3,2558 |
|
m2 (M¤ ) |
0,2442 |
|
A (R¤ ) |
3,694 |
|
R1 (R¤ ) |
2,23 |
|
R2 (R¤ ) |
0,57 |
|
tömegátadási ráta (M¤ /év) |
5*10-8 |
|
q spektroszkópiai |
0,075 |
7. táblázat: Az AW UMa általam meghatározott fizikai paraméterei
A komponensek effektív hômérséklete T1= 7100 illetve T2= 6900K körüli érték, ami az irodalomban meghatározott színképtípusnak megfelelô érték. Az adatok alapján a fôkomponens felületi fényessége nagyobb, így a rendszer ún. A-típusú. A kapott eredmények jó egyezést mutatnak az irodalmi értékekkel.
A rendszer alapos ismerete nagy motivációt adott egy kevésbé ismert kettôs fénygörbéjének modellezéséhez. Az illesztés végeredményeként bebizonyosodott számításaim hitelessége. A modellezés során kapott fázisdiagram jó egyezést mutat a mért fényességváltozással. Így a felhasznált modellezô prog-ram megfelelônek bizonyult a kevésbé ismert rendszer analízisére.
II. FU Dra érintkezô kettôscsillag
Az általam vizsgált kettôscsillagról eddig a Hipparcos katalógusban szereplô adatokon kívül semmilyen mérési eredményt nem publikáltak. A Bajai Obszervatóriumban készített képek kiértékelésével összeállítottam az FU Dra fénygörbéjét, mely alapján a heliocentrikus korrekciót is figyelembe véve új minimum-idôpontokat határoztam meg:
Tmin II = 2451722.4762 HJD
Tmin II = 2451723.3979 HJD
Az O-C diagram segítségével perióduskorrekciót végeztem, melynek alapján az új korrigált periódus Púj = 0,3067169 nap.
A fázisdiagrammról az alábbiak olvashatók le:
1. az amplitudó: 0,47 magnitúdó
2. a két minimum különbözô fényességû, az eltérés csak 0,025 magnitúdó értékû, de már kimutatható.
3. 0,5 fázisnál a minimum halványabb, konstans
4. 1,0 fázisnál pedig fényesebb, „hegyes"
Ebbôl adódóan 0,5 fázisnál totális fedés, 1,0 fázisnál gyûrûs fedés állapítható meg. A kisebb komponens felületi fényessége nagyobb.Tehát gyakorlatilag majdnem merôlegesen látunk rá a forgástengelyre (az inklináció közel 90o). A fénygörbe-modellezés során meggyôzô bizonyítékot kaptam: valóban teljes fedést mutat a rendszer, az inklináció 80,8º (az eltérés azzal magyarázható, hogy a kontaktus miatt már kisebb pályahajlásnál is bekövetkezik a teljes fedés).
A radiális sebesség görbe amplitúdójából kiszámoltam a rendszer spektroszkópiai tömegarányát. Ezen érték, az általam korrigált periódus és a fénygörbe-modellezés eredményéül kapott inklináció ismeretében a rendszer össztömegét és a komponensek tömegeit is meghatároztam.
Számításaim eredményeit a 8. táblázat foglalja össze:
|
Pkorrigált (nap) |
0,3067178 |
|
i ( º ) |
80,8 |
|
M (M¤ ) |
1,44 |
|
m1 (M¤ ) |
0,29 |
|
m2 (M¤ ) |
1,15 |
|
qspektroszkópiai |
0,25 |
8. táblázat: Az FU Dra általam meghatározott fizikai paraméterei
A modellezés eredményeként a komponensek effektív hômérséklete T1= 6200 illetve T2= 6505 K körüli érték, azaz a mellékkomponens hômérséklete kicsit nagyobb, bizonyítva a kontakt rendszer W-típusba történô besorolását.
A tanulmányozott kettôs rendszerek fizikai paramétereinek meghatározása közvetlenül felhasználható eredményeket szolgáltat ezen rendszerek csillagfejlôdési állapotának tanulmányozásához.
Munkám folytatásaként további kettôs rendszerekrôl szeretnék többszín-fotometriai és spektroszkópiai méréseket végezni.
Köszönetnyilvánítás
Ezúton is szeretném köszönetemet kifejezni Dr. Vinkó Józsefnek, aki tudományos vezetôként segítette munkámat, Dr. Kiss Lászlónak, a mérendô csillag kiválasztásában valamint a készített képek redukálásában nyújtott segítségéért. Köszönettel tartozom Fûrész Gábornak és Csák Balázsnak a mérésekben illetve az adatfeldolgozásban való önzetlen és segítôkész közremûködésükért, valamint Dr. Hegedüs Tibornak, a Bajai Obszervatórium igazgatójának az észlelésekhez szükséges távcsôidô biztosításáért.
Irodalomjegyzék
Binnendijk, L. 1970, Vistas in Astronomy 12, 217
Carroll, W., Ostlie, L. 1996, Introduction to Modern Astrophysics
Derman, E., Demircan, O., Müyesseroglu, Z. 1990, IBVS No. 3540
Dupree, A.K. 1983, Activity in Red Dwarf Stars (ed. P.B.Byrne, M.Rodono) p. 441
Eggen, O. 1967, Mem R.A.S. 70, 111
Fûrész, G. 1998, Rövid periódusú változócsillagok keresése galaktikus nyílthalmazokban, TDK-dolgozat, JATE
Hegedüs, T. 1988, Bull. Inf. CDS No.35.
Hrivnak, B.J. 1982, ApJ 260, 744
Kopal, Z. 1978, Dynamics of Close Binary Systems (D.Reidel)
Kuiper, A. 1941, ApJ 93, 133
Lucy, L.B. 1968, ApJ 151, 1123
Lucy, L.B. 1973, Astroph. & Sp.Sci. 22, 381
McLean, B.J. 1981, MNRAS 195, 931
Mochnacki, S.W., Doughty, N.A.. 1972, MNRAS 156, 51
Nagy T.A. 1974, PhD thesis, University of Pennsylvania
Paczynski, B. 1964, AJ 69, 124
Rucinksi, S.M., Lu, W., Mochnacki, S.W. 2000, AJ 120, 1133
Wilson, R.E., Devinney, E.J. 1973, ApJ 182, 539
|

