Fedési és pulzáló változócsillagok periódusvizsgálata
2006
A fedési és pulzáló változócsillagok egyik legfontosabb paramétere a fényváltozás periódusa. Sok esetben a megfigyelhetõ fényességváltozás szigorúan periodikusan ismétlõdik, más esetben pedig felépíthetõ különbözõ periódusú komponensek összegeként. Bármelyik esetet is tekintjük, általában éveken, évtizedeken átívelõ megfigyelési sorozatok szükségesek a pontos periodicitások meghatározására. Különösen érdekesek azok az esetek, ahol a periódus megváltozik. Ilyenkor a változások jellege elárulhatja azok okát, például a csillagfejlõdési hatásokat, vagy kettõs rendszerben történõ keringést.
Jelen dolgozatban olyan vizsgálatokat mutatok be, melyek 2000 és 2002 között elvégzett fényességméréseken alapulnak. Az általam tanulmányozott változócsillagok többsége egyszeresen periodikus fényváltozású, így méréseimmel az évtizedes idõskálájú periódusváltozásokat tudtam megvizsgálni. Két esetben a rövidperiódusú pulzáló csillagok többszörös periodicitását találtam, amelyet a többmódusú pulzáció jeleként értelmeztem.
Diákköri dolgozatom felépítése a következõ. Legelõször röviden áttekintem az egyszeres és többszörös periodicitás jelentését a változócsillagok esetében. Ismertetem a tanulmányozott két fõ változócsillag-osztály, a fedési és pulzáló változócsillagok legfontosabb tulajdonságait. Ezek után a bõ másfél év során használt mûszereket ismertetem, kezdve a Szegedi Csillagvizsgáló távcsöveitõl egészen a Sierra Nevadai Obszervatórium mûszeréig. Mivel munkámon végigvonul az  diagram alkalmazása, röviden tárgyalom a módszer néhány egyszerû tulajdonságát. diagram alkalmazása, röviden tárgyalom a módszer néhány egyszerû tulajdonságát.
A dolgozatom gerincét az eredmények ismertetése teszi ki. Elsõként a fedési kettõscsillagokkal kapcsolatos vizsgálataimat részletezem, melyekben a periódusvizsgálatok mellett néhány egyszerû többszín-fotometriai meggondolás is megjelenik. Legtöbb megfigyelést 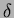 Scuti-típusú csillagokról végeztem, így munkám közel felét az északi ég 11 magnitúdónál fényesebb nagyamplitúdójú Scuti-típusú csillagokról végeztem, így munkám közel felét az északi ég 11 magnitúdónál fényesebb nagyamplitúdójú 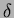 Scuti-csillagainak fotometriai felmérése és az elsõ eredmények bemutatása teszi ki. Végezetül egy többszörösen periodikus Scuti-csillagainak fotometriai felmérése és az elsõ eredmények bemutatása teszi ki. Végezetül egy többszörösen periodikus 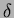 Scuti-csillag, a V784 Cassiopeiae frekvencia-analízisét mutatom be. Scuti-csillag, a V784 Cassiopeiae frekvencia-analízisét mutatom be.
Diákköri munkámat rövid összefoglalással fejezem be. A 2000 augusztusa és 2002 januárja között elvégzett mérések segítségével alapos betekintést nyertem a rövidperiódusú változócsillagok közé, melynek részleteit az itt következõ oldalakon olvashatjuk.
Dolgozatomban változócsillagok fényváltozását vizsgáltam saját, valamint irodalmi mérési adatok alapján. Mivel vizsgálataim elsõdleges célja a fénygörbék periodicitásának, illetve annak finom változásainak kimutatása és értelmezése, ebben a pontban röviden összefoglalnám, hogy milyen alapjelenségek felelnek a változások sokszor alig 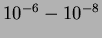 -os relatív ingadozással mérhetõ periodicitásaiért. Elõször az alapfogalmakat adom meg. -os relatív ingadozással mérhetõ periodicitásaiért. Elõször az alapfogalmakat adom meg.
Változócsillagok egyszeres periodicitása alatt azt értjük, ha a csillag bizonyos paramétere (például fényessége, radiális sebessége) egy bizonyos idõintervallumban ismétlõdõen ugyanolyan mértékben változik, azaz szigorúan periodikus változást mutat. Az ilyen ismétlõdõ változások három fõ ok miatt jöhetnek létre:
1. két csillag egymás körüli keringése;
2. a csillag pulzációja;
3. a csillag tengely körüli forgása.
Kettõscsillagok esetén a keringés során a csillagok radiális sebességének periodikus változása figyelhetõ meg. Ha mozgásuk pályájára úgy látunk rá, hogy elfedik egymást, akkor periodikus fényességcsökkenéseket is megfigyelhetünk.
Egy csillag pulzációja azt jelenti, hogy a csillag változtatja sugarát (radiális pulzáció) és/vagy felszínének szomszédos tartományai különbözõ fázisban mozognak (nemradiális pulzáció), gyakran igen szigorú periodicitást mutatva. Ez mind radiális sebesség, mind fényességméréssel kimutatható.
A csillagok tengely körüli forgása is okozhat periodikus változásokat. Ha egy csillag felszínén elég nagy folt található, akkor a tengelyforgás következtében ciklikus fényességváltozásokat figyelhetünk meg. Ezek a foltok több tucat rotációs periódus során fennmaradhatnak. Jól ismert forgási változócsillagok például a neutroncsillagok, melyekben a mágneses és a forgási tengely nem esik egybe. A mágneses tengely változó láthatóságának és a csillag hihetetlenül gyors tengelyforgásának következtében nagyon szabályos változások mutathatók ki széles hullámhossztartományban (rádiótól a röntgen hullámhosszakig). A változások nagyon rövid idõskálán (másodperc vagy annak törtrésze alatt) játszódnak le. Ezeket az objektumokat nevezzük pulzároknak.
A többszörös periodicitás fogalma azt jelenti, hogy a csillagban megfigyelt változásokat több, hasonló vagy akár különbözõ okból eredõ periodikus folyamat okozza. Pulzáló változócsillagoknál nagyon gyakori jelenség, hogy a fénygörbén a pulzáció amplitúdójában hosszabb-rövidebb periódusú modulációja figyelhetõ meg.
A többszörös periodicitású jelenségeket két nagyobb csoportra oszthatjuk, ha a kiváltó tényezõ alapján vizsgálódunk:
1. nem pulzációs eredetû;
2. pulzációs eredetû.
Az elsõ csoportba olyan csillagtípusokat értünk, amelyek esetén a pulzációs eredetû fényváltozások mellett rotációból vagy kitörésekbõl származó változások is megfigyelhetõek. Ezenkívül számos fedési és spektroszkópiai kettõscsillagot ismerünk, ahol az egyik vagy olykor mindkét komponens pulzál (Szatmáry 1987).
A második csoportba olyan csillagokat sorolunk, amelyekben több frekvenciájú pulzáció (radiális és nem radiális módus) is egyidejûleg van jelen. Ez alapján tovább oszthatjuk ezt a csoportot a módusok gerjesztettsége szerint. Így három alcsoportot szokás megkülönböztetni:
a. csak radiális módusok,
b. radiális és nemradiális módusok,
c. csak nemradiális módusok
vannak gerjesztve.
A radiális módusok együttes gerjesztettsége például a cefeidákra jellemzõ. Leggyakrabban az alapmódus és az elsõ felhang fordul elõ, de azért akad példa az alapmódus és második felhang, valamint az elsõ és második felhang együttes jelenlétére (Kiss 1999).
Radiális és nemradiális módosok együttes jelenlétét általában 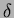 Scuti- és Scuti- és 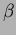 Cephei-típusú változóknál mutatják ki. Cephei-típusú változóknál mutatják ki.
Nemradiális módusok pulzáló fehér törpék, valamint a gyorsan oszcilláló Ap-típusú változók körében jellemzõ. Számos csillag esetén sikerült már kimutatni akár néhány perces oszcillációkat. Ezek alapján egyre inkább úgy tûnik, hogy valamennyi csillag rezeg a sajátfrekvenciáin, csak sok esetben a mai méréstechnikákkal ez nem detektálható.
A pulzáló változócsillagok sok típusánál találunk többszörös periodicitást. Ennek jelentõsége, hogy az elméleti modellekkel való összehasonlítás (számított periódusok és periódusarányok) révén meghatározhatók a vizsgált csillagok legfontosabb asztrofizikai paraméterei (ez az asztroszeizmológia feladata).
Ebben a fejezetben rövid áttekintést igyekszem adni az általam vizsgált két fõ változócsillag-típusról a fedési kettõsökrõl, valamint a pulzáló 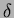 Scuti-típusú csillagokról. Scuti-típusú csillagokról.
A kettõscsillagok számos típusa közül most a fedési kettõsöket jellemzem. A fedési kettõsök olyan tömegközéppontjuk körül keringõ csillagok, amelyeknél majdnem pontosan a keringési síkban látunk rá a pályára. Ennek következtében a komponensek elfedik egymást, ezért a kettõsség egyértelmûen kimutatható a fénygörbébõl. Ebben az esetben a fénygörbe alakja elsõsorban a csillagok szeparációjától és pályájuk inklinációjától függ.
A fénygörbék alakja szerint három alosztályba sorolhatók a fedési kettõscsillagok:
1. Algol-típus, amelyekre jellemzõ, hogy a két gömb alakú (vagy csak kevésbé eltorzult) komponens közti távolság jóval meghaladja a két csillag sugarát. Ennek következtében fedésen kívül állandó, míg fedéskor hirtelen csökkenõ fényességet tapasztalhatunk. A fõminimumban akár több magnitúdós is lehet a fényességcsökkenés, a mellékminimum viszont nem igen haladja meg a tizedmagnitúdót sem. Elõfordul olyan eset is ennél a típusnál, hogy annyira különbözõ felületi fényességûek a komponensek, hogy a mellékminimum alig különböztethetõ meg a fénygörbe állandó fényességû szakaszától.
A fõ- és mellékminimum idõbeli viszonyát erõsen befolyásolhatja a pálya excentricitása. Körpálya (e=0) esetén a mellékminimum két fõminimum között félúton helyezkedik el. Nagy excentricitás (0 e<1) esetén ettõl eléggé eltérõ helyen figyelhetõ meg a mellékminimum. e<1) esetén ettõl eléggé eltérõ helyen figyelhetõ meg a mellékminimum.
A legkülönbözõbb keringési periódusok fordulnak elõ 0,2 naptól akár 10000 napig.
2. A 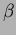 Lyrae-típusú fedési kettõsök komponensei ellipszoidális alakúak. Az összfényesség folyamatosan változik, a fedés kezdete és vége nem határozható meg pontosan. Ezeknél a csillagoknál mindig látszik a mellékminimum is, ami mindig kisebb mélységû a fõminimumnál. Lyrae-típusú fedési kettõsök komponensei ellipszoidális alakúak. Az összfényesség folyamatosan változik, a fedés kezdete és vége nem határozható meg pontosan. Ezeknél a csillagoknál mindig látszik a mellékminimum is, ami mindig kisebb mélységû a fõminimumnál.
A fényváltozási amplitúdó általában kisebb 2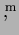 0-nál, periódusuk pedig hosszabb egy napnál. 0-nál, periódusuk pedig hosszabb egy napnál.
3. A W UMa-típusú fedési kettõscsillagok két egymáshoz nagyon hasonló, ellipszoidális komponensbõl állnak. Periódusuk rövidebb egy napnál, leginkább a 0,2 és 0,4 nap közötti érték jellemzõ. A fénygörbéjükön a fõ- és mellékminimum közel egyforma mély és folyamatosan változik a fényesség.
Dolgozatomban a fedési kettõsök három típusához tartozó csillagok közül kettõvel foglalkoztam: egy Algol-típusúval, amely hosszú periódusú (P 1277 nap), és eléggé excentrikus (e=0,55) pályán mozog, valamint két, közel nyolc órás periódussal keringõ W UMa-típusú változóval. 1277 nap), és eléggé excentrikus (e=0,55) pályán mozog, valamint két, közel nyolc órás periódussal keringõ W UMa-típusú változóval.
A pulzáló változócsillagoknál a fényesség idõbeli változását a csillag méretének és hõmérsékletének változása okozza. Ezen belül számos altípust különböztetünk meg. Ebben a fejezetben az egyik leggyakrabban elõforduló pulzáló csillagfajtát, a 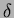 Scuti-csillagok fõ jellemzõit mutatom be, mivel megfigyeléseim nagy részét ez a típus képezi. Scuti-csillagok fõ jellemzõit mutatom be, mivel megfigyeléseim nagy részét ez a típus képezi.
A 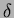 Scuti-típusú változók a Hertzsprung-Russell-diagram ún. instabilitási sávjában helyezkednek el, közel a fõsorozathoz. Fiatal, közepes tömegû (1 Scuti-típusú változók a Hertzsprung-Russell-diagram ún. instabilitási sávjában helyezkednek el, közel a fõsorozathoz. Fiatal, közepes tömegû (1 2 M 2 M ), A ), A F (T F (T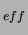 =7000 =7000  9000 K) színképtípusú törpe, esetleg szubóriás (általában 9000 K) színképtípusú törpe, esetleg szubóriás (általában  1 1 2 R 2 R ) csillagok. Néhány órás periódussal és néhány század-, egy-két tizedmagnitúdós amplitúdóval pulzálnak. Gyakran fordul elõ, hogy fénygörbéjük többszörös periodicitású, amelynek oka, hogy egyszerre több módus gerjesztett. Radiális és nemradiális módusok egyaránt kimutathatóak, amelyek egyértelmûen csak nagyfelbontású spektroszkópia segítségével különböztethetõek meg. Elméleti modellek alapján a frekvenciaarányokból is azonosítják az egyes módusok fajtáit. ) csillagok. Néhány órás periódussal és néhány század-, egy-két tizedmagnitúdós amplitúdóval pulzálnak. Gyakran fordul elõ, hogy fénygörbéjük többszörös periodicitású, amelynek oka, hogy egyszerre több módus gerjesztett. Radiális és nemradiális módusok egyaránt kimutathatóak, amelyek egyértelmûen csak nagyfelbontású spektroszkópia segítségével különböztethetõek meg. Elméleti modellek alapján a frekvenciaarányokból is azonosítják az egyes módusok fajtáit.
Mivel dolgozatom nagy részét a 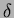 Scuti-csillagok egy csoportja teszi ki, ezért megemlítem még, hogy szokás a Scuti-csillagok egy csoportja teszi ki, ezért megemlítem még, hogy szokás a 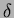 Scuti-csillagokon belül egy családot megkülönböztetni, amelyeket nagyamplitúdójú Scuti-csillagokon belül egy családot megkülönböztetni, amelyeket nagyamplitúdójú 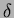 Scuti-változóknak hívnak. Ebbe a családba jórészt monoperiodikus változók tartoznak, periódusuk jellemzõen 0,1 nap körüli, amplitúdójuk pedig 0 Scuti-változóknak hívnak. Ebbe a családba jórészt monoperiodikus változók tartoznak, periódusuk jellemzõen 0,1 nap körüli, amplitúdójuk pedig 0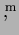 4 4 0 0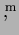 6 közé esik. A nagyamplitúdójú 6 közé esik. A nagyamplitúdójú 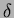 Scuti-csillagoknak létezik II. populációs megfelelõje, amelyeket SX Phoenicis-típusú változóknak neveznek. Scuti-csillagoknak létezik II. populációs megfelelõje, amelyeket SX Phoenicis-típusú változóknak neveznek.
Ebben az alfejezetben azokat a mûszereket mutatom be, amelyekkel méréseimet végeztem. A távcsöveket átmérõjük szerint növekvõ sorrendben ismertetem. A címekben szereplõ rövidítések az alkalmazott mûszereket kódolják: késõbb röviden ezekkel hivatkozok rájuk.
A távcsõ a Szegedi Tudományegyetem Béke épületének tetején található. Egy 28 cm-es belépõ nyílású f/6,3 Schmidt-Cassegrain-típusú távcsõ. A mûszert a Celestron cég gyártotta, mechanikája ekvatoriális szerelésû. A mérésemkor a képek felvételére egy SBIG ST 9E típusú CCD kamerát használtam. Ennek fõ jellemzõi: 512 9E típusú CCD kamerát használtam. Ennek fõ jellemzõi: 512 512 pixel, 20 512 pixel, 20 20 20 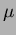 -os pixelméret, 16 bites AD konverter. -os pixelméret, 16 bites AD konverter.
1. ábra: A 28 cm-es távcsõ és ST  9 kamera
A Szegedi Csillagvizsgáló mérõmûszere, amely a város szélén található. A távcsõ f/14-es fényerejû, 40 cm-es átmérõjû és Cassegrain-típusú1(l. Fûrész 2000). A mechanika ekvatoriális szerelésû. A detektor ugyanaz az SBIG ST 9E típusú CCD kamera, amelyet a 28 cm-es távcsõnél használtam. A méréseket a Johnson-féle fotometriai rendszer szûrõivel végeztem. 9E típusú CCD kamera, amelyet a 28 cm-es távcsõnél használtam. A méréseket a Johnson-féle fotometriai rendszer szûrõivel végeztem.
2. ábra: A Szegedi Csillagvizsgáló 40 cm-es távcsöve
A Johnson-féle rendszer
A legelterjedtebb fotometriai rendszert kezdetben UBV szûrõket definiálták. Késõbb kiterjesztették az infravörös tartományra is a rendszert az R, I, J, K, L, M és N szûrõkkel. A rendszer szélessávú (  ) szûrõket tartalmaz, melyek közül a BVRI szûrõket használtam. Fõbb adataikat az 1. táblázat tartalmazza. ) szûrõket tartalmaz, melyek közül a BVRI szûrõket használtam. Fõbb adataikat az 1. táblázat tartalmazza.
| szûrõ |
központi hullámhossz (nm) |
sávszélesség (nm) |
| B |
440 |
100 |
| V |
550 |
90 |
| R |
700 |
200 |
| I |
850 |
230 |
1. táblázat: A Johnson-rendszer transzmissziós függvényei
A közvetlenül mért, úgynevezett instrumentális magnitúdókat a standard fotometriai rendszerbe lineáris transzformációkkal visszük át, melyek differenciális esetben a következõ alakúak (Henden és Kaitchuk 1982):
Ezekben az egyenletekben a B, V, R, I értékek standard fényességadatok, míg a b, v, r, i értékek instrumentális magnitúdók. Az 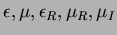 együtthatókat transzformációs együtthatóknak (vagy távcsõkonstansoknak) hívjuk. együtthatókat transzformációs együtthatóknak (vagy távcsõkonstansoknak) hívjuk.
Saját méréseket végeztem annak érdekében, hogy a szegedi 40 cm-es távcsõ transzformációs együtthatóit meghatározzam. Ehhez az M67 nyílthalmaz fotometriai standard csillagait használtam fel (Chevalier és Ilovaisky 1991). Ennek alapján a 2. táblázatban szereplõ transzformációs együtthatókat határoztam meg a távcsõre.
Jól látszik, hogy az ideális esethez képest ( 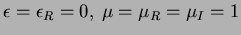 ) a szegedi szûrõk által definiált rendszer kicsit eltér a standardtól. Mindazonáltal a távcsõkonstansokat megadó összefüggések a vizsgált színtartományban nagy pontossággal lineárisak, így a standard transzformációk megbízhatóan alkalmazhatók. ) a szegedi szûrõk által definiált rendszer kicsit eltér a standardtól. Mindazonáltal a távcsõkonstansokat megadó összefüggések a vizsgált színtartományban nagy pontossággal lineárisak, így a standard transzformációk megbízhatóan alkalmazhatók.
| együttható jele |
együttható értéke |
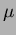 |
1,131 0,061 0,061 |
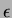 |
0,113 0,039 0,039 |
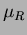 |
1,230 0,093 0,093 |
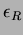 |
0,215 0,074 0,074 |
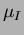 |
1,063 0,036 0,036 |
2. táblázat: A Szegedi Obszervatórium 40 cm-es távcsövének transzformációs együtthatói
Méréseim egy részét az MTA Csillagászati Kutatóintézet Piszkéstetõi Obszervatóriumának f/3-as, Schmidt-típusú távcsövével végeztem. A távcsõ belépõ nyílása 60 cm, a tükör átmérõje 90 cm, mechanikája villás parallaktikus. A detektor Photometrics AT 200 CCD kamera. Paraméterei: 200 CCD kamera. Paraméterei: 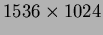 pixel, pixelmérete 9 pixel, pixelmérete 9 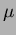 , 14 bites, AD konverter. Az elért látómezõ , 14 bites, AD konverter. Az elért látómezõ 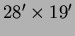 . .
A Piszkéstetõi Obszervatórium mûszerére is meghatároztam a transzformációs együtthatókat, amelyeket a következõ táblázatban foglalok össze:
| együttható jele |
együttható értéke |
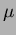 |
0,925 0,030 0,030 |
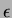 |
0,098 0,038 0,038 |
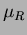 |
1,037 0,038 0,038 |
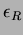 |
0,219 0,077 0,077 |
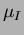 |
1,011 0,033 0,033 |
3. táblázat: a Piszkéstetõi Obszervatórium Schmidt-távcsövének transzformációs együtthatói
3. ábra: A Piszkéstetõi Obszervatórium Schmidt távcsöve
A spanyolországi Insituto de Astrofísica de Andalucía Sierra Nevadai Obszervatóriumának 90 cm-es távcsövét 2001 nyarán két héten keresztül használtam méréseimhez. Az obszervatórium tengerszint feletti magassága 2896 m. A mûszer 90 cm-es átmérõjû f/8-as Ritchey-Chrétien-típusú. A detektor egy négycsatornás spektrofotométer, amely a Strömgren-féle fotometriai rendszert valósítja meg. A mérésekhez 28 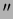 -os apertúrát használtam. -os apertúrát használtam.
4. ábra: A Sierra Nevadai Obszervatórium 90 cm-es távcsöve és fotométere
A Strömgren-rendszer
A Strömgren-rendszer közepes sávszélességû szûrõket használ, ezek az u - ultraibolya, v - ibolya, b - kék, y - sárga. Az effektív hullámhosszakat a 4. táblázatban mutatom be.
| szûrõ |
központi hullámhossz (nm) |
sávszéleség (nm) |
| u |
350 |
34 |
| v |
410 |
20 |
| b |
470 |
16 |
| y |
550 |
24 |
4. táblázat: Strömgren szûrõk legfontosabb adatai (Kiss 1999)
Ennek a rendszernek számos elõnye van a Johnson-féle rendszerrel szemben. Ezek közül most csak azt emelném ki, hogy a 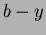 színindex megbízhatóbb hõmérséklet indikátor a színindex megbízhatóbb hõmérséklet indikátor a 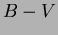 színindexnél. színindexnél.
Mivel a Strömgren-rendszer színindexei kevert indexek, azaz színindexek különbségei, így a standard transzformáció más alakot ölt. Ezen kívül az y szûrõt úgy választották meg, hogy központi hullámhossza megegyezzen a Johnson V szûrõével, ezért tulajdonképp standard ``y'' fényesség nincs is, a transzformációs egyenletek Johnson-féle V-t adnak. Tehát a standard transzformációs egyenletek differenciális fotometria esetén így alakulnak (Kiss 1999):
ahol 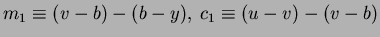
Mivel a v szûrõ lefedi a hõmérséklettel erõsen változó H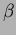 vonalat, ezért a vonal abszorpciós hatását a standard transzformációk extra vonalat, ezért a vonal abszorpciós hatását a standard transzformációk extra 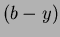 -tól függõ tagjaival vehetjük figyelembe. Az A, B, C, D, E, és F transzformációs együtthatók ismert fényességû csillagok segítségével mérhetõk ki. A Sierra Nevada Obszervatórium esetén ezek az együtthatók a következõk (Rodríguez, személyes közlés): -tól függõ tagjaival vehetjük figyelembe. Az A, B, C, D, E, és F transzformációs együtthatók ismert fényességû csillagok segítségével mérhetõk ki. A Sierra Nevada Obszervatórium esetén ezek az együtthatók a következõk (Rodríguez, személyes közlés):
| együttható |
A |
B |
C |
D |
E |
F |
| értéke |
0,021 |
0,975 |
0,730 |
0,049 |
1,058 |
0,201 |
5. táblázat: A transzformációs együtthatók
Ebben a pontban röviden ismertetem, hogyan történt a CCD képek feldolgozása, azaz milyen módon jutothattam el a képek felvételétõl a kész fénygörbékig.
A CCD képekbõl az apertúra fotometria segítségével kaptam olyan adatokat, amelyekbõl el lehetett készíteni a fénygörbéket. Az apertúra fotometriát az IRAF noao/ digiphot/ apphot csomagjával végeztem. Itt csak azokat a paramétereket írom le, amelyeket minden egyes éjszaka képkiméréseinél változtatni kell.
Mielõtt a képeket kimértem, elvégeztem a képek flatkorrekcióját. Ez egy nagyon fontos korrekció, mert ennek segítségével tudjuk figyelembe venni az CCD egyes pixeleinek különbözõ mértékû érzékenységét, amely erõsen befolyásolhatja a mérési eredményeket. Ennek elvégzésére a flatképek normált átlagát az imsum task-kal lehet elkészíteni, amelyben a flatképek listáját kell megadnunk bemenõ paraméterként, kimenõként pedig azt a nevet, amelyet adni szeretnénk flatképünknek. Maga a flatkorrekció (amely során pixelenként osztjuk el az egyes képeket a flatképpel) a noao/ imred/ ccdred csomag ccdproc taskjával történik. Ebben a taskban csak a képek listáját és azt a flatképet kell megadnunk, amellyel korrigálni akarunk.
A képek kiméréséhez elõször is a daofind taskot használtam. Ennek a tasknak az a feladata, hogy egy CCD képen csillagokat keressen, és az egyes képeken megtalált csillagok adatait egy coo.1 kiterjesztésû file-ban tárolja. Ahhoz, hogy elvégezhesse feladatát, bizonyos paramétereket meg kell adnunk, amelyek a jellemzik az adott éjszaka képeit. Egy taskot az epar paranccsal lehet módosítani. A következõ paramétereket kell meghatározni és értékeiket beírni a task paraméterlistájába:
-image: A képek listája.
-output: Itt a kimenetet lehet megadni. Ha default-ban hagyjuk, akkor coo.1 kiterjesztésû file-ok lesznek a kimenetben.
-datapars: Tulajdonképp ebben adjuk meg a képekre jellemzõ paramétereket. A következõket kell módosítani. Az fwhmpsf paraméterben a csillagok félértékszélességét, a sigma paraméterben a képek hátterének szórását kell megadni. Ezekhez a datapars-ból a :e billentyûkombinációval juthatunk.
-findpars: Ebben adhatjuk meg, hogy a háttérbõl hányszoros szórással kiemelkedõ intenzitásértéket fogadja el csillagként.
Ezeket a paramétereket az imexam task-kal lehet meghatározni, amely ebbõl a csomagból is elindítható. Ezt futtatva, és az r billentyû leütésével egy csillag intenzitás-eloszlásáról radiális ábrát kaphatunk a pixelek (adott pixeltõl való távolság) függvényében. Ennek során kiírja a képernyõre a félértékszélességet, amelyet a datapars taskban hasznosítunk. Errõl a radiális ábráról lehet leolvasni egy késõbbi paramétert, hogy mekkora apertúrát kell majd használnunk magához a fotometriához. Ezen kívül most még fontos számunkra a kiméréshez az m billentyû lenyomására futó program, amely statisztikát ír ki a képernyõre egy 5 5-ös négyzetrõl. Ezzel kapunk felvilágosítást a háttér szórásáról. 5-ös négyzetrõl. Ezzel kapunk felvilágosítást a háttér szórásáról.
A daofind task a :g paranccsal futtatható. Ennek lefutásával már egy kicsit felgyorsulnak az események. Megvannak az egyes képeken talált csillagok listája. A következõ lépés ezen csillagok instrumentális magnitúdóinak meghatározása. Ez a phot task-kal történik. Ebben a következõ paramétereket kell megadni:
-photpar: Az az apertúraméret, amellyel történik a fotometria. Amikor meghatározzuk ezt a paramétert, nagyon figyelmesnek kell lenni, mivel túl kis méretû apertúrát megadva a kimaradt részek intenzitása kiesik, ha pedig túl nagy az apertúra, akkor zajnövelõ módon a hátteret is belevesszük a fotometriába.
-fitskypar: Ebben az apertúra minden egyes méretét megadhatjuk, azaz a gyûrû belsõ sugarát, vastagságát. A saját kiméréseimhez 3 pixel vastagságú apertúrát használtam.
Ezek után futtathatjuk a fotometriát. A futás végén mag.1 kiterjesztésû file-okban találhatóak a kapott fényességek.
A két task lefutásával létrejövõ file-ok számos adatot tartalmaznak a képekrõl. Számomra a fénygörbék elkészítéséhez csak a fényességértékekre volt szükség, olykor pedig a csillagok koordinátáira. A keresett adatokat a txdump task-kal lehet kiszedni a file-okból. Ebben a taskban csak a bemenõ (textfile) paramétert kell megadni, azaz azoknak a file-oknak a listáját, amelyek tartalmazzák a számunkra lényeges adatokat. Ezenkívül azokat a paraméterneveket kell beírni, amelyeket ki szeretnénk szedni a file-okból. Ezt a fields paraméterben tehetjük meg. Ebben és a képek neveivel (image) együtt a fényeségeket (mag), valamint ha szükséges volt a csillagok koordinátáit (xcenter, ycenter) írattam ki. Ennek a task-nak a futási eredményét célszerû nem a képernyõre, hanem egy file-ba átirányítani.
Ahhoz, hogy megkapjam a fénygörbéket, szükséges volt még az egyes fényességpontokhoz tartozó idõpontok meghatározása. Ezt a noao/ imred/ kpnocoude csomag setjd task-jának segítségével lehet elvégezni. Ez a task a képek fejlécében található idõpontokból és koordinátákból meghatározza a Julián-dátumot és a heliocentrikus Julián-dátumot. Ebben is csak a képek listáját kell megadni, majd a futtatást egy file-ba szoktam vezetni.
A fénygörbékhez szükséges adatokat egy Pascal program futtatásával nyertem ki. Ennek a programnak egyszerû a mûködése. Két file-ból (egyik az egyes képek neveit és az azokhoz tartozó idõpontokat tartalmazza, másik pedig a képek neveit és a rajtuk talált csillagok magnitúdói fényesség szerint rendezve) képzi a megfelelõ képek idõpontját és ahhoz a megfelelõ differenciális magnitúdóértékeket. Azért lehet ilyen egyszerûen megalkotni a fénygörbét, mert a megfigyeléseim során elkészített CCD képeken a változócsillag egy esetet kivéve mindig a legfényesebb csillag a látómezõben, összehasonlítókként pedig rendre a látómezõ második, illetve harmadik legfényesebb csillagait választottam. Az egyetlen kivételes eset a V567 Ophiuchi volt, ahol maximumban a legfényesebb, minimumban a második legfényesebb csillag volt a látómezõben. Ebben az esetben a koordináták figyelembevételével készítettem el az adatokat.
Az  diagram elkészítéséhez szükség van a fénygörbék maximumának vagy minimumának meghatározására. Ezt is egy Pascal program segítségével határoztam meg, amely a fénygörbék maximumának illetve minimumának környezetére alacsony fokszámú (általában ötödfokú) polinomot illeszt és ennek szélsõértékét határozza meg. diagram elkészítéséhez szükség van a fénygörbék maximumának vagy minimumának meghatározására. Ezt is egy Pascal program segítségével határoztam meg, amely a fénygörbék maximumának illetve minimumának környezetére alacsony fokszámú (általában ötödfokú) polinomot illeszt és ennek szélsõértékét határozza meg.
Az egyszeresen periodikus csillagok vizsgálatában a nagy múltra visszatekintõ, hagyományos  módszert alkalmaztam. Mivel ez a módszer a periodikus folyamatok tárgyalása esetén széles körben alkalmazható és magam is szinte minden esetben ezt használtam, fontosnak éreztem, hogy részletesebben tárgyaljam a módszer alapjait és néhány legfontosabb tulajdonságát. módszert alkalmaztam. Mivel ez a módszer a periodikus folyamatok tárgyalása esetén széles körben alkalmazható és magam is szinte minden esetben ezt használtam, fontosnak éreztem, hogy részletesebben tárgyaljam a módszer alapjait és néhány legfontosabb tulajdonságát.
Az  diagram a szigorúan periodikusan lejátszódó folyamatok vizsgálatának egyik eszköze, amellyel nagyon pontos ( diagram a szigorúan periodikusan lejátszódó folyamatok vizsgálatának egyik eszköze, amellyel nagyon pontos ( 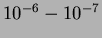 relatív pontosságú) periódusmeghatározás lehetséges, illetve segítségével vizsgálhatók a periódus finom változásai. relatív pontosságú) periódusmeghatározás lehetséges, illetve segítségével vizsgálhatók a periódus finom változásai.
Alapfeltevése a következõ:
Legyen ismert egy a vizsgált csillagászati jelenségre jellemzõ idõpont (epocha, 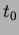 : pl. a maximális vagy minimális fényesség idõpontja), valamint az ekkor érvényes periódus értéke ( : pl. a maximális vagy minimális fényesség idõpontja), valamint az ekkor érvényes periódus értéke ( 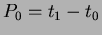 : két egymást követõ maximum vagy minimum közt eltelt idõ). A mérésekbõl meg lehet határozni a fényességmaximum, illetve fényességminimum bekövetkezésének pillanatát. Így rendelkezésünkre áll egy megfigyelt idõpont (O=obszervált). Ezt össze lehet hasonlítani az adott fénygörbejelenség bekövetkezésének számított (C=calculated) idõpontjával. Ezt az epocha és a számítások szerint azóta eltelt idõ összegeként kapjuk. Ez utóbbit úgy tudjuk megkapni, hogy a periódusra elfogadott értéket beszorozzuk az adott epochától lezajlott ciklusok számával. Így a következõ módon definiálhatjuk egy tetszõleges megfigyelt maximum- vagy minimumidõpontban ( : két egymást követõ maximum vagy minimum közt eltelt idõ). A mérésekbõl meg lehet határozni a fényességmaximum, illetve fényességminimum bekövetkezésének pillanatát. Így rendelkezésünkre áll egy megfigyelt idõpont (O=obszervált). Ezt össze lehet hasonlítani az adott fénygörbejelenség bekövetkezésének számított (C=calculated) idõpontjával. Ezt az epocha és a számítások szerint azóta eltelt idõ összegeként kapjuk. Ez utóbbit úgy tudjuk megkapni, hogy a periódusra elfogadott értéket beszorozzuk az adott epochától lezajlott ciklusok számával. Így a következõ módon definiálhatjuk egy tetszõleges megfigyelt maximum- vagy minimumidõpontban (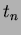 ) az ) az  értékét: értékét:
ahol 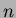 a ciklusszám. a ciklusszám.
A megfigyelt (O) és a számított (C) idõpont közötti különbséget az idõ vagy a ciklusszám függvényében ábrázolva kapjuk az  diagramot. diagramot.
Az  diagram vizsgálatában néhány egyszerû esetet különböztetünk meg. Legyen diagram vizsgálatában néhány egyszerû esetet különböztetünk meg. Legyen 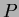 a fényességváltozás valódi periódusa, a fényességváltozás valódi periódusa, 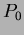 pedig az pedig az  diagram számításához használt periódus. diagram számításához használt periódus.
1. 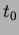 , , 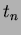 ismert, ismert, 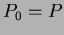 állandók állandók
Ekkor az 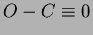 egyenes. Az idõpont meghatározás pontatlanságai miatt az egyenes. Az idõpont meghatározás pontatlanságai miatt az  pontok az egyenes körül szórnak. pontok az egyenes körül szórnak.
2. 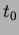 , , 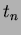 ismert, ismert, 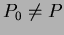 állandók állandók
Ekkor 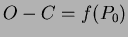 : :
Két esetet lehet megkülönböztetni:
a.) Ha a 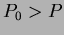 , akkor az , akkor az 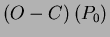 kisebb lesz, mint amit az kisebb lesz, mint amit az 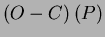 -vel számolnánk. Így egy negatív meredekségû egyenest kapunk. -vel számolnánk. Így egy negatív meredekségû egyenest kapunk.
b.) Ha a 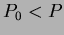 , akkor az , akkor az 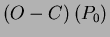 nagyobb értékeket vesz fel, mint amit az nagyobb értékeket vesz fel, mint amit az 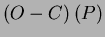 -vel számolnánk. Így egy pozitív meredekségû egyenest kapunk. -vel számolnánk. Így egy pozitív meredekségû egyenest kapunk.
Az 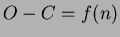 kvázifolytonos függvényként is értelmezhetõ. Legyen kvázifolytonos függvényként is értelmezhetõ. Legyen 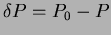 ! !
Az egyenlet utolsó részében a zárójeles tag 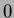 -t ad (mivel a helyes periódussal számoljuk az -t ad (mivel a helyes periódussal számoljuk az  értéket, lásd 1. eset), a maradék pedig egy egyenest ad. Ebbõl értéket, lásd 1. eset), a maradék pedig egy egyenest ad. Ebbõl
amely tulajdonképp az  diagram meredeksége. Megfelelõ módon korrigálva a meredekséggel, megkapjuk a helyes periódusértéket. diagram meredeksége. Megfelelõ módon korrigálva a meredekséggel, megkapjuk a helyes periódusértéket.
3. Vizsgáljuk meg azt az esetet, ha a periódus egyenletesen változik! Legyen ez most az egyenletes periódusnövekedés esete! Változzon a periódus (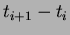 ) ciklusonként ) ciklusonként 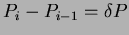 -vel! Ekkor az n-edik megfigyelt idõpont a következõképp adódik: -vel! Ekkor az n-edik megfigyelt idõpont a következõképp adódik:
Számítsuk ki az  diagramot valamilyen diagramot valamilyen 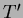 és és 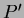 efemerissel! Ekkor a számított idõpont: efemerissel! Ekkor a számított idõpont:
ahol 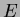 az az 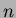 ciklusszám becsült értéke, amelynek meghatározása nagy jelentõségû az ciklusszám becsült értéke, amelynek meghatározása nagy jelentõségû az  diagram elkészítésében. Egyértelmû megadása akkor lehetséges, ha a megfigyelt adatsorban lévõ ûrök idõtartama alatt nem változik a periódus nagy mértékben. diagram elkészítésében. Egyértelmû megadása akkor lehetséges, ha a megfigyelt adatsorban lévõ ûrök idõtartama alatt nem változik a periódus nagy mértékben.
Tegyük fel, hogy  , , 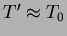 és és 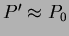 ! Így a definíció alapján: ! Így a definíció alapján:
Tehát az egyenletes periódusváltozás esetén az  diagram másodfokú függvény lesz. Az diagram másodfokú függvény lesz. Az  pontokra parabolát illesztve számíthatóak lesznek a korrekcióhoz szükséges paraméterek: pontokra parabolát illesztve számíthatóak lesznek a korrekcióhoz szükséges paraméterek:
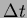 : epocha-korrekció : epocha-korrekció
 : periódus-korrekció : periódus-korrekció
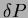 : periódusváltozási ráta, amelyet : periódusváltozási ráta, amelyet 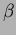 -val is szoktak jelölni -val is szoktak jelölni
Megjegyzés: A 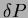 az elsõfokú tagban is szerepel, de ez elhanyagolhatóan kicsi általában a az elsõfokú tagban is szerepel, de ez elhanyagolhatóan kicsi általában a  -hez képest. -hez képest.
Az  -re kapott formulából kitûnik, hogy csak diszkrét idõpontokban van értelmezve. Ennek ellenére az -re kapott formulából kitûnik, hogy csak diszkrét idõpontokban van értelmezve. Ennek ellenére az  diagramot kvázifolytonosnak tekinthetjük, ha elegendõen sok cikluson keresztül, azaz nagy idõintervallumban vizsgáljuk a periódusváltozást. diagramot kvázifolytonosnak tekinthetjük, ha elegendõen sok cikluson keresztül, azaz nagy idõintervallumban vizsgáljuk a periódusváltozást.
Fény-idõ effektus
Ha egy pulzáló változócsillag egy kettõs rendszer tagja, akkor pályájának különbözõ szakaszain látszólag más-más pulzációs periódus észlelhetõ. A tömegközéppont körüli keringés miatt a periódus hossza periodikus változást mutat. Ez az  diagram alakjából kimutatható. A keringés során a vizsgált csillag távolsága változik a megfigyelõhöz képest, így a csillagról kisugárzott fénynek változó nagyságú utat kell megtennie a pálya egyes szakaszain, azaz a kisugárzott jel frekvenciája periodikus modulációt szenved. Ezt a jelenséget hívjuk fény-idõ effektusnak. A változócsillag diagram alakjából kimutatható. A keringés során a vizsgált csillag távolsága változik a megfigyelõhöz képest, így a csillagról kisugárzott fénynek változó nagyságú utat kell megtennie a pálya egyes szakaszain, azaz a kisugárzott jel frekvenciája periodikus modulációt szenved. Ezt a jelenséget hívjuk fény-idõ effektusnak. A változócsillag  diagramja ekkor a látóirányra merõleges síktól vett, idõben változó távolságától függ, feltéve, hogy a csillagnak nincs saját periódusváltozása. diagramja ekkor a látóirányra merõleges síktól vett, idõben változó távolságától függ, feltéve, hogy a csillagnak nincs saját periódusváltozása.
Legyen a periodikus jelforrás egy kettõs rendszerben és mozogjon 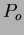 orbitális periódussal! Ebben az esetben egy orbitális periódussal! Ebben az esetben egy 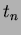 idõpontban idõpontban
ahol 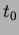 a rögzített epocha, a rögzített epocha, 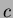 a fénysebesség, a fénysebesség, 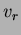 a radiális sebesség, a radiális sebesség, 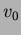 a tömegközéppont radiális sebessége. Tehát az a tömegközéppont radiális sebessége. Tehát az  diagram a radiális sebesség görbe integrálja. Ebbõl égi mechanikai számításokkal kapjuk az diagram a radiális sebesség görbe integrálja. Ebbõl égi mechanikai számításokkal kapjuk az  -re a következõ formulát (levezetését l. Szatmáry 1987): -re a következõ formulát (levezetését l. Szatmáry 1987):
ahol 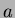 a félnagytengely, a félnagytengely, 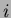 az inklináció, az inklináció, 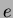 a numerikus excentricitás, a numerikus excentricitás, 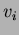 a valódi anomália, a valódi anomália, 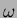 a pericentrum hosszúsága. a pericentrum hosszúsága.
Figyelembe véve, hogy a valódi anomália idõfüggéséhez az excentrikus anomálián és a Kepler-egyenlet numerikus megoldásán keresztül jutunk el (Marik 1989), adódik a következtetés, hogy az  diagram idõfüggésére nincs zárt, analitikus formula. Gyakorlatban a megfigyelt diagram idõfüggésére nincs zárt, analitikus formula. Gyakorlatban a megfigyelt  diagramokat illesztjük a fenti elméleti alakkal, amelybõl három pályaelem adódik. diagramokat illesztjük a fenti elméleti alakkal, amelybõl három pályaelem adódik.
A dolgozatom gerincét adó fejezetben részletesen ismertetem a három év mérésein alapuló eredményeket. Elõször a fedési kettõscsillagokat tárgyalom, majd következnek a legfontosabb kutatási eredményekhez veze | 
